Solveeit Logo
Login

Question

Question: Let us assume that a sphere of mass \(1kg\) rests at one corner of a cube. The cube has been moved w...

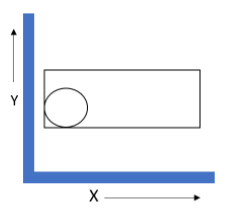
Let us assume that a sphere of mass 1kg1kg rests at one corner of a cube. The cube has been moved with a velocity v⃗=8ti^−2t2j^\vec{v}=8t\hat{i}-2{{t}^{2}}\hat{j} where tt be time in second. What will be the force by sphere on the cube at t=1t=1? (g=10ms−2)\left( g=10m{{s}^{-2}} \right) [The diagram represents the vertical plane of the cube].

A.8N B.10N C.20N D.45N \begin{aligned} & A.8N \\\ & B.10N \\\ & C.20N \\\ & D.4\sqrt{5}N \\\ \end{aligned}

Explanation

Solution

Acceleration of the cube will be found by taking the derivative of this equation of velocity. The pseudo force on the sphere will be found by taking the product of the mass of the sphere and the acceleration of the sphere. The magnitude of the force will be the square root of magnitude of each component of the force. This will help you in answering this question.

Complete answer: It has been given that the cube is moving with a velocity given as,
v⃗=8ti^−2t2j^\vec{v}=8t\hat{i}-2{{t}^{2}}\hat{j}
Acceleration of the cube will be found by taking the derivative of this equation of velocity. That is,
a=dvdt=8i^−4tj^a=\dfrac{dv}{dt}=8\hat{i}-4t\hat{j}
It has been mentioned in the question that the time taken be,
t=1t=1
Substituting this in the equation will give,
a=8i^−4j^a=8\hat{i}-4\hat{j}
The pseudo force on the sphere will be given as
F=−mdvdtF=-m\dfrac{dv}{dt}
Where mm is the mass of the sphere.
The mass of the sphere has been mentioned in the question as,
m=1kgm=1kg
Substituting the acceleration and mass of the sphere in the equation of force will give,
F=−8i^+4j^F=-8\hat{i}+4\hat{j}
Therefore the magnitude of the force will be the square root of magnitude of each component of the force. That is,
∣F⃗∣=64+16=80=45N\left| {\vec{F}} \right|=\sqrt{64+16}=\sqrt{80}=4\sqrt{5}N
Therefore the magnitude of the force in this situation has been calculated.

The correct answer has been mentioned as option D.

Note:
The acceleration can be defined as the rate of variation in the velocity of the body with respect to the time taken. The velocity of the body can be defined as the rate of variation of the displacement with respect to time taken. Both these quantities are vectors having both magnitude and direction.