Question

Let us assume that a ring of radius $r$ and mass per unit length $m$ is found to be rotating with an angular velocity $\omega$ in a free space. What will be the tension in the ring?
$\begin{aligned} & A.zero \\\ & B.\dfrac{1}{2}m{{\omega }^{2}}{{r}^{2}} \\\ & C.m{{\omega }^{2}}{{r}^{2}} \\\ & D.m{{\omega }^{2}}r \\\ \end{aligned}$

Answer 1

Find out the resultant force mass of the section AB. for a circular motion, the centripetal force will be equivalent to the product of the mass of the body, radius of the path taken and the square of the angular velocity in a free space. Substitute the values obtained in this and rearrange the equation. This will help you in answering this question.

Complete step by step answer:
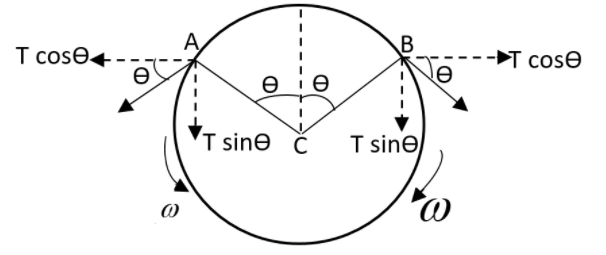
First of all let us assume that $T$ be the tension in the string. For the section AB mentioned in the diagram, the resultant force is found to be
$F=2T\sin \theta$
As the angle $\theta$ is very small, we can consider,
$\sin \theta \approx \theta$
Therefore the resultant force can be written as,
$F=2T\theta$
This net force has been found to be towards C.
The mass of the section AB can be written as,
$M=2r\theta m$
As we all know, for a circular motion, the centripetal force will be equivalent to the product of the mass of the body, radius of the path taken and the square of the angular velocity in a free space. That is we can write that,
$F=mr{{\omega }^{2}}$
As here we can substitute the values we have obtained, we can write that,
$2T\theta =\left( 2r\theta m \right)r{{\omega }^{2}}$
Rearranging this equation will give,
$T=m{{r}^{2}}{{\omega }^{2}}$

So, the correct answer is “Option C”.

Note: Tension can be defined as the kind of force which is being axially transmitted by the help of a string, chain, a cable or similar one-dimensional continuous body. As this is similar to the force, the unit as well as the dimension of both these quantities are similar. The force and tension has been expressed in newton.