Solveeit Logo
Login

Question

Question: Let us assume that a person can see clearly only up to a distance of 25cm. He needs to read a book w...

Let us assume that a person can see clearly only up to a distance of 25cm. He needs to read a book which has been kept at a distance of 50cm50cm. What kind of lens does he need for his spectacles and also calculate its power?
A.concave,−1D B.convex,+1.5D C.concave,−2.0D D.convex,+2.0D \begin{aligned} & A.\text{concave},-1D \\\ & B.\text{convex},+1.5D \\\ & C.\text{concave},-2.0D \\\ & D.\text{convex},+2.0D \\\ \end{aligned}

Explanation

Solution

The object distance of the object from the lens will be equivalent to the distance up to which we want to see. The image distance from the lens will be equivalent to the distance up to which we can see. The power of the lens will be the reciprocal of the focal length of the lens. This will help you in answering this question.

Complete step by step solution:
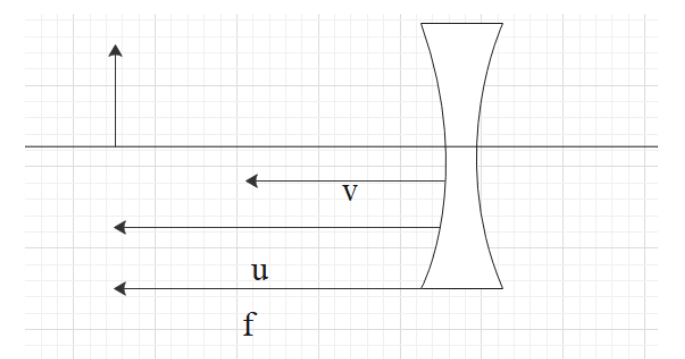
From the descriptions given in the question, we can surely say that the person is suffering from the condition called myopia. In order to correct the condition of myopia, he must use a lens of concave nature. Therefore we can write that,
The object distance of the object from the lens will be equivalent to the distance up to which we want to see. Therefore as it is mentioned in the question, we can write that,
u=−50cmu=-50cm
The image distance from the lens will be equivalent to the distance up to which we can see. Therefore we can write that,
v=−25cmv=-25cm
Lens equation can be written as,
1f=1v−1u\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}
Substituting the values in the equation will give,
1f=1−25−1−50 ⇒f=−50cm \begin{aligned} & \dfrac{1}{f}=\dfrac{1}{-25}-\dfrac{1}{-50} \\\ & \Rightarrow f=-50cm \\\ \end{aligned}
Therefore the focal length of the lens used has been obtained. From this also as the sign is negative we can confirm that the lens used will be concave.
The power of the lens will be the reciprocal of the focal length of the lens. This can be shown as,
P=1f=100−50m=−2DP=\dfrac{1}{f}=\dfrac{100}{-50m}=-2D

So, the correct answer is “Option C”.

Note: The reciprocal of the focal length of the lens will be equivalent to the difference between the reciprocal of the image distance and the reciprocal of the object distance. This is the lens equation. The sign convention is to be considered perfectly in order to solve this question.