Solveeit Logo
Login

Question

Question: Let us assume that a man can swim at the rate of \(5km{{h}^{-1}}\) in the still water. A \(1km\) wid...

Let us assume that a man can swim at the rate of 5kmh−15km{{h}^{-1}} in the still water. A 1km1km wide river is flowing at the rate of 3kmh−13km{{h}^{-1}}. The man who is wishing in order to swim across the river which is directly opposite to the starting point.
A. Along what direction should the man swim?
B. What must be his resultant velocity?
C. How much time will the man take to cross the river?

Explanation

Solution

The resultant velocity of the man can be found by taking the square root of the difference between the squares of the velocity of the man in still water and the river. Time taken to cross the river will be equivalent to the ratio of the width of the river and the resultant velocity of the man. This will help you in answering this question.

Complete answer:
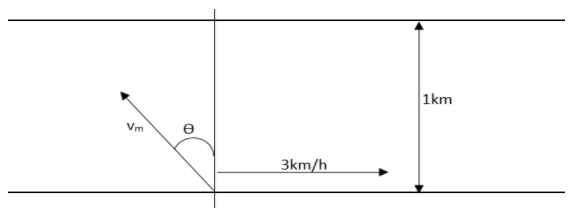
A. the velocity of the man with respect to the river water, v=5kmh−1v=5km{{h}^{-1}}. This will be greater than the river flow velocity. Hence he will be crossing the river directly (along the shortest path or no drift condition from the flow velocity). The angle of swim can be shown as,
θ=π2+sin⁡−1(uv)\theta =\dfrac{\pi }{2}+{{\sin }^{-1}}\left( \dfrac{u}{v} \right)
That is,
θ=90∘+sin⁡−1(uv)\theta =90{}^\circ +{{\sin }^{-1}}\left( \dfrac{u}{v} \right)
It has been given in the question that,
The velocity of the river flowing can be written as,
u=3kmh−1u=3km{{h}^{-1}}
The velocity of the man swimming in the still water can be shown as,
v=5kmh−1v=5km{{h}^{-1}}
Substituting this values in the equation can be shown as,
θ=90∘+sin⁡−1(35)=90∘+37∘=127∘\theta =90{}^\circ +{{\sin }^{-1}}\left( \dfrac{3}{5} \right)=90{}^\circ +37{}^\circ =127{}^\circ
That means, 127∘127{}^\circ with respect to the river flow and 37∘37{}^\circ with respect to the perpendicular in the upstream direction.
B. Resultant velocity or velocity of man will be found as,
vm=v2−u2{{v}_{m}}=\sqrt{{{v}^{2}}-{{u}^{2}}}
Substituting the values in this equation can be shown as,
vm=52−32=4kmh−1{{v}_{m}}=\sqrt{{{5}^{2}}-{{3}^{2}}}=4km{{h}^{-1}}
This will be in a direction which is perpendicular to the flow of the river.
C. time taken to cross the river will be found by,
t=dv2−u2=1km4kmh−1=14h=15min⁡t=\dfrac{d}{\sqrt{{{v}^{2}}-{{u}^{2}}}}=\dfrac{1km}{4km{{h}^{-1}}}=\dfrac{1}{4}h=15\min
Hence the question has been solved.

Note:
Relative velocity can be defined as the velocity of a body B in the rest frame of the other object A. In mathematical way, the relative velocity will be the vector difference between the velocities of two objects. A vector will be having both the magnitude and the direction.