Question
Question: let us assume that a cylindrical container of radius \(R\) and height \(h\) is fully filled with a l...
let us assume that a cylindrical container of radius R and height h is fully filled with a liquid. It has been connected to two horizontal L shaped pipes having a small cross-sectional area a to the cylinder as shown in the diagram. Now let us assume that these two pipes are opened and fluid begins to come out of the pipes horizontally in opposite directions. Then what will be the torque due to ejected liquid on the system?
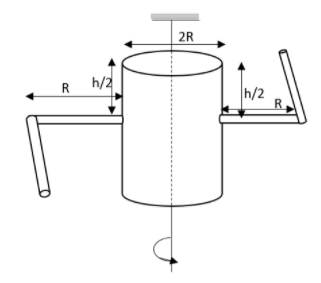
A.4aghρRB.8aghρRC.2aghρRD.none of these
Solution
The velocity of efflux of water can be found by taking the square root of twice the product of the acceleration due to gravity and the height of the liquid. Here the force on the ejected water will be equivalent to the rate of variation of momentum of the ejected water. This will help you in answering this question.
Complete step by step answer:
the velocity of efflux of water can be found by taking the square root of twice the product of the acceleration due to gravity and the height of the liquid. Here the height of the liquid can be shown as,
h→2h
This can be written as,
V=2g2h=gh
Here the force on the ejected water will be equivalent to the rate of variation of momentum of the ejected water.
That is,
F=ρaV2
Where ρbe the density of liquid, a be the cross sectional area and Vbe the velocity of efflux.
Therefore the torque of these forces about the central line will be equivalent to,
τ=(ρaV2)×4R
Simplifying this equation can be done as,
τ=4ρaV2R
Substituting the velocity of efflux in the equation can be shown as,
τ=4ρaghR
Hence the torque due to ejected liquid on the system has been obtained.
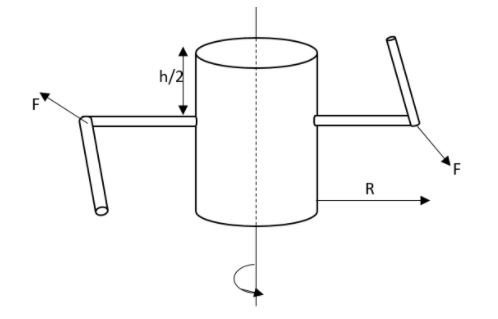
So, the correct answer is “Option A”.
Note: Velocity of efflux is not dependable on the size of orifice. The density of the fluid will be actually changing with depth for greater heights. In such situations, the velocity of efflux will be dependable on the density of the liquid.
