Question

Let us assume that a ball is released from the top of a tower of height $h$ metres. It takes $T$ seconds to reach the ground. What will be the position of the ball in $\dfrac{T}{3}$ seconds?

Answer 1

The initial velocity of the ball will be at zero as the ball is just released from the tower. Newton's second equation of motion is to be applied here. The displacement of the body can be found by taking the sum of the product of the initial velocity and time taken and half the product of acceleration due to gravity and square of the time taken. This will help you in answering this question.

Complete answer:

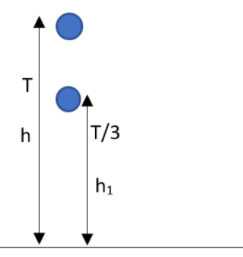
Let us assume that the acceleration of the ball be $g$. The initial velocity of the ball will be at zero as the ball is just released from the tower. Therefore we can write that,
$u=0$
The time taken will be given as $T$. The body will be travelling a height mentioned to be as $h$ metres. By the application of equation of motion, we can write that,
$s=uT+\dfrac{1}{2}g{{T}^{2}}$
Substituting the values mentioned in the question here will give,
$h=\dfrac{1}{2}g{{T}^{2}}$.......... (1)
In $\dfrac{T}{3}$ seconds, the height traversed by the ball can be represented as ${{h}_{1}}$. Therefore we can write that,
${{h}_{1}}=\dfrac{1}{2}g\left( \dfrac{{{T}^{2}}}{3} \right)$
Simplifying this equation can be written as,
${{h}_{1}}=\dfrac{1}{2}g{{T}^{2}}\times \dfrac{1}{9}$………. (2)
From the equation (1) and (2) we can write that,
$h=\dfrac{{{h}_{1}}}{9}$
Where this is the distance from the point of release.
Hence the distance from the ground can be found to be as,
$d=h-{{h}_{1}}$
Substituting the values in it will give,
$d=h-\dfrac{h}{9}=\dfrac{8h}{9}$
Therefore the answer has been calculated.

Note:
The acceleration of a body is defined to be the variation in velocity with respect to the time taken. The velocity is defined to be the variation in displacement of a body with respect to the time taken. The displacement is the shortest distance between the initial and final positions of the body.