Question

Let $\underset{x\to 0}{\mathop{\lim }}\,{{\sec }^{-1}}\left( \dfrac{x}{\sin x} \right)=l$ and $\underset{x\to 0}{\mathop{\lim }}\,{{\sec }^{-1}}\left( \dfrac{x}{\tan x} \right)=m$, then
(a) l exists but m does not
(b) m exists but l does not
(c) l and m both exist
(d) neither l nor m exists

Answer 1

Hint: Relate the relation between x, sin x and tan x when x is limiting to zero. Relate it with the domain of ${{\sec }^{-1}}x$ for existing limits.

Here, we have given the limits as
$\underset{x\to 0}{\mathop{\lim }}\,{{\sec }^{-1}}\left( \dfrac{x}{\sin x} \right)=l....\left( i \right)$
And, $\underset{x\to 0}{\mathop{\lim }}\,{{\sec }^{-1}}\left( \dfrac{x}{\tan x} \right)=m.....\left( ii \right)$
First, we need to know about the domain of ${{\sec }^{-1}}x$ i.e. $\left( -\infty ,-1 \right]\cup \left[ 1,\infty \right)$.
Now, try to relate values of $\dfrac{x}{\sin x}$ and $\dfrac{x}{\tan x}$ for limit $x\to 0$, if value inside of ${{\sec }^{-1}}\left( {} \right)$ will lie in $\left( -1,1 \right)$ then limit will not exist and if value inside the bracket lies in $\left( -\infty ,-1 \right]\cup \left[ 1,\infty \right)$. Hence limit will exist.
Let us first relate $\dfrac{x}{\sin x}$.
One can relate x with sin x and tan x by calculating tangent equations of tan x and sin x at (0, 0) and relate it with y = x.
We know that one can find tangent at any point lying on the curve by calculating slope at that point. Let the point be $\left( {{x}_{1}},{{y}_{1}} \right)$ and curve is y = f (x) then tangent at $\left( {{x}_{1}},{{y}_{1}} \right)$ can be given by $y-{{y}_{1}}={{\left. \dfrac{dy}{dx} \right|}_{\left( {{x}_{1}},{{y}_{1}} \right)}}\left( x-{{x}_{1}} \right)$
Tangent equation for sin x at (0, 0) is
$y-0={{\left. \dfrac{d}{dx}\left( \sin x \right) \right|}_{\left( 0,0 \right)}}\left( x-0 \right)$
$y={{\left. \cos x \right|}_{\left( 0,0 \right)}}\left( x \right)\text{ }\left[ \because \dfrac{d}{dx}\sin x=\cos x \right]$
$y=x$
Hence, $y=x$ is tangent for $y=\sin x$.
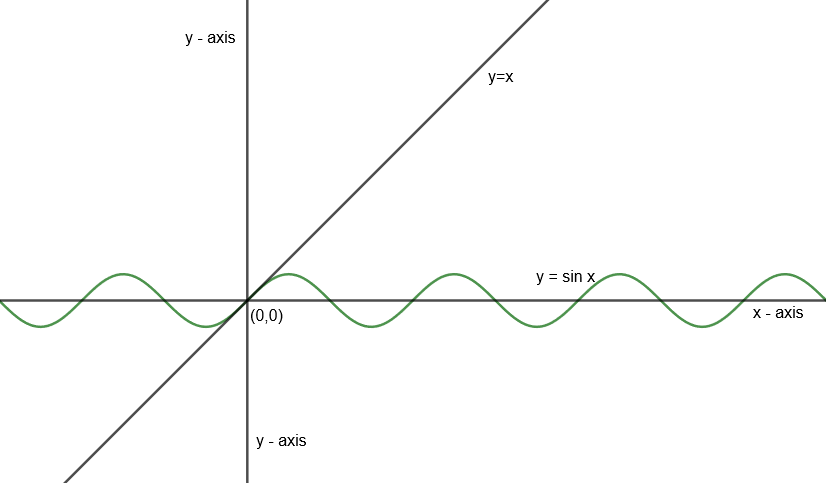
Draw graph of x and sin x in one coordinate plane as follows:

Now for the second case i.e. $\dfrac{x}{\tan x}$, we get the tangent equation of tan x at (0, 0) is
$y-0={{\left. \dfrac{dy}{dx} \right|}_{\left( 0,0 \right)}}\left( x-0 \right)$
$y={{\left. {{\sec }^{2}}x \right|}_{\left( 0,0 \right)}}\left( x \right)\text{ }\left[ \dfrac{d}{dx}\tan x={{\sec }^{2}}x \right]$
$y=x$
Hence, y = x is tangent for $y=\tan x$ as well.
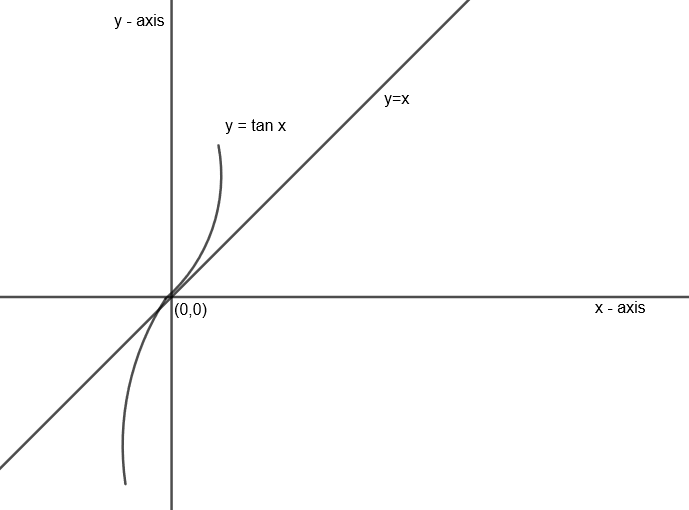
Let us draw the graph of x and tan x as follows:
Now from the graphs, we can relate for $\dfrac{x}{\sin x}$ that is:
Case 1: $x\to {{0}^{+}}$
We observe x > sin x
Hence, $\dfrac{x}{\sin x}>1$
Case 2: $x\to {{0}^{-}}$
Here, sin x has a higher positive magnitude than x. Hence, if we put a negative sign to both x and sin x, then
$x>\sin x$
$\dfrac{x}{\sin x}>1$
Hence, from case 1 and case 2, we get
If $\lim x\to 0,$ then $\dfrac{x}{\sin x}>1....\left( iii \right)$
Similarly, let us relate x and tan x for $x\to 0$
Case 1: $x\to {{0}^{+}}$
x < tan x
$\dfrac{x}{\tan x}<1$
Case 2: $x\to {{0}^{-}}$
x < tan x
$\dfrac{x}{\tan x}<1$
Hence, for $x\to 0$, we have $\dfrac{x}{\tan x}<1....\left( iv \right)$
Now, for limit ‘l’ from equation (i), we get
$l=\underset{x\to 0}{\mathop{\lim }}\,{{\sec }^{-1}}\left( \dfrac{x}{\sin x} \right)$
As we have $\dfrac{x}{\sin x}>1$ from equation (iii) and domain of ${{\sec }^{-1}}x$ is $\left( -\infty ,-1 \right]\cup \left[ 1,\infty \right)$ as explained in the starting. Hence, we can put $\lim x\to 0$ to the given relation.
So, $l=\underset{x\to 0}{\mathop{\lim }}\,{{\sec }^{-1}}\left( \dfrac{x}{\sin x} \right)$ will exist.
For limit ‘m’ from equation (ii), we get
$m=\underset{x\to 0}{\mathop{\lim }}\,{{\sec }^{-1}}\left( \dfrac{x}{\tan x} \right)$
We have already calculated that $\dfrac{x}{\tan x}<1$ from equation (iv) and domain of ${{\sec }^{-1}}x$ is $\left( -\infty ,-1 \right]\cup \left[ 1,\infty \right)$. Hence the given limit will not exist.
Hence, option (a) is the correct answer to the given problem.

Note: One can directly put $\underset{x\to 0}{\mathop{\lim }}\,\dfrac{x}{\sin x}=1$ and $\underset{x\to 0}{\mathop{\lim }}\,\dfrac{x}{\tan x}=1$ as we generally use but that will be wrong for the given expression. As the exact value of $\underset{x\to 0}{\mathop{\lim }}\,\dfrac{x}{\sin x}$ and $\underset{x\to 0}{\mathop{\lim }}\,\dfrac{x}{\tan x}$ is not exactly 1, it’s the limiting value of the given expressions. Hence, be careful with these kinds of problems. Relating x with tan x and sin x by calculating tangent at (0, 0) for sin x and tan x is the key point of the question.