Solveeit Logo
Login

Question

Question: Let $U_n = \int_{0}^{\frac{\pi}{2}} x \sin^n x dx$, then find the value of $\left( \frac{100U_{10}-1...

Let Un=∫0π2xsin⁡nxdxU_n = \int_{0}^{\frac{\pi}{2}} x \sin^n x dx, then find the value of (100U10−1U8)\left( \frac{100U_{10}-1}{U_8} \right).

Answer

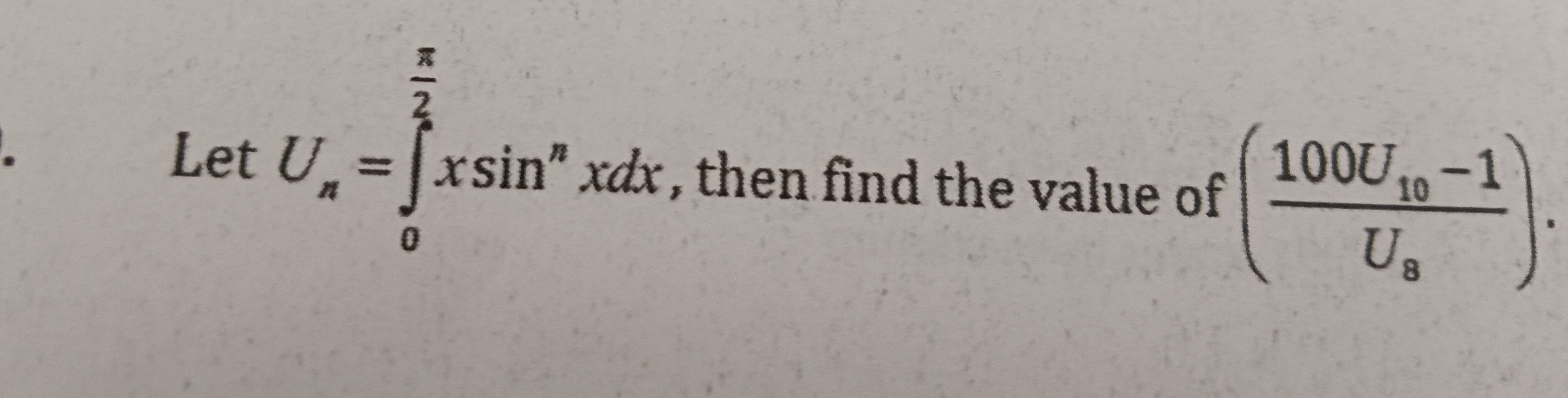
90

Explanation

Solution

To find the value of (100U10−1U8)\left( \frac{100U_{10}-1}{U_8} \right), we first need to establish a reduction formula for Un=∫0π2xsin⁡nxdxU_n = \int_{0}^{\frac{\pi}{2}} x \sin^n x dx. We use integration by parts with u=xsin⁡n−1xu = x \sin^{n-1} x and dv=sin⁡xdxdv = \sin x dx. This gives du=(sin⁡n−1x+x(n−1)sin⁡n−2xcos⁡x)dxdu = \left( \sin^{n-1} x + x(n-1)\sin^{n-2} x \cos x \right) dx and v=−cos⁡xv = -\cos x.

Applying the integration by parts formula ∫u dv=uv−∫v du\int u \, dv = uv - \int v \, du: Un=[xsin⁡n−1x(−cos⁡x)]0π2−∫0π2(−cos⁡x)(sin⁡n−1x+x(n−1)sin⁡n−2xcos⁡x)dxU_n = \left[ x \sin^{n-1} x (-\cos x) \right]_0^{\frac{\pi}{2}} - \int_{0}^{\frac{\pi}{2}} (-\cos x) \left( \sin^{n-1} x + x(n-1)\sin^{n-2} x \cos x \right) dx

The boundary term [−xsin⁡n−1xcos⁡x]0π2\left[ -x \sin^{n-1} x \cos x \right]_0^{\frac{\pi}{2}} evaluates to 0.

So, Un=∫0π2cos⁡xsin⁡n−1xdx+(n−1)∫0π2xsin⁡n−2xcos⁡2xdxU_n = \int_{0}^{\frac{\pi}{2}} \cos x \sin^{n-1} x dx + (n-1) \int_{0}^{\frac{\pi}{2}} x \sin^{n-2} x \cos^2 x dx.

The first integral ∫0π2cos⁡xsin⁡n−1xdx\int_{0}^{\frac{\pi}{2}} \cos x \sin^{n-1} x dx can be solved using the substitution t=sin⁡xt = \sin x, which yields 1n\frac{1}{n}.

The second integral can be rewritten as (n−1)∫0π2xsin⁡n−2x(1−sin⁡2x)dx=(n−1)(∫0π2xsin⁡n−2xdx−∫0π2xsin⁡nxdx)=(n−1)(Un−2−Un)(n-1) \int_{0}^{\frac{\pi}{2}} x \sin^{n-2} x (1-\sin^2 x) dx = (n-1) \left( \int_{0}^{\frac{\pi}{2}} x \sin^{n-2} x dx - \int_{0}^{\frac{\pi}{2}} x \sin^n x dx \right) = (n-1) (U_{n-2} - U_n).

Substituting these results back into the expression for UnU_n: Un=1n+(n−1)(Un−2−Un)U_n = \frac{1}{n} + (n-1) (U_{n-2} - U_n) Un=1n+(n−1)Un−2−(n−1)UnU_n = \frac{1}{n} + (n-1) U_{n-2} - (n-1) U_n nUn=1n+(n−1)Un−2n U_n = \frac{1}{n} + (n-1) U_{n-2}.

Now, we apply this reduction formula for n=10n=10: 10U10=110+(10−1)U10−210 U_{10} = \frac{1}{10} + (10-1) U_{10-2} 10U10=110+9U810 U_{10} = \frac{1}{10} + 9 U_8.

To obtain the numerator 100U10−1100U_{10}-1, we multiply the equation by 10: 10×(10U10)=10×(110+9U8)10 \times (10 U_{10}) = 10 \times \left( \frac{1}{10} + 9 U_8 \right) 100U10=1+90U8100 U_{10} = 1 + 90 U_8.

Rearranging this equation gives: 100U10−1=90U8100 U_{10} - 1 = 90 U_8.

Finally, we substitute this into the expression we need to evaluate: 100U10−1U8=90U8U8\frac{100U_{10}-1}{U_8} = \frac{90 U_8}{U_8}.

Since U8=∫0π2xsin⁡8xdxU_8 = \int_{0}^{\frac{\pi}{2}} x \sin^8 x dx is positive for x∈(0,π2)x \in (0, \frac{\pi}{2}), we can cancel U8U_8: 90U8U8=90\frac{90 U_8}{U_8} = 90.