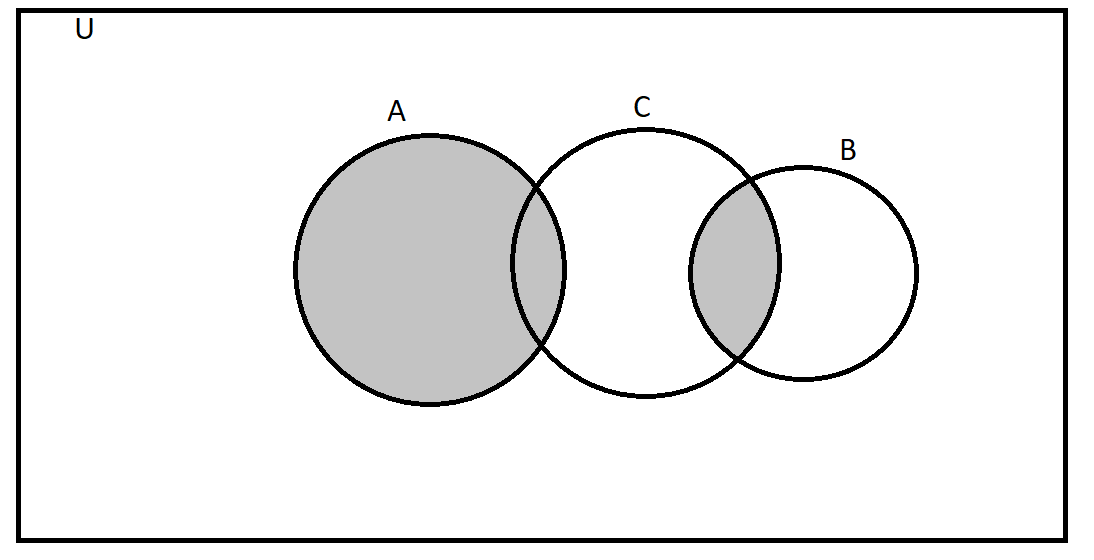
Question
Question: Let U the universal set be the set of all students of a school. A is a set of boys. B is a set of gi...
Let U the universal set be the set of all students of a school. A is a set of boys. B is a set of girls, and C is the set of students participating in sports. Describe the following set in words and represent it by Venn diagram
A⋃(B⋂C)
Solution
Hint: Union of the two sets A and B is a set which contains all the elements of A and B and none of the elements which are not present in both the sets. Hence if x is in Union of A and B then x is in A or x is in B.The intersection of two sets A and B is a set which contains all the elements present in both A and B and none of the elements which are not present in either of the two sets A and B. Hence if x is in the intersection of A and B then x is in both A and B.
Complete step-by-step answer:
Keeping in mind, the above definitions of union and intersection think what elements does the set A⋃(B⋂C) contain.
Draw the corresponding Venn diagram. Note that the set of girls and Boys are disjoint
Let x is in A⋃(B⋂C).
Hence from the definition of the union of two sets we have x is in A or x is in B⋂C.
Hence from the definition of the intersection of two sets, we have x is in A or (x is in B and x is in C).
Hence either x is a boy or x is a girl playing sports.
Hence A⋃(B⋂C) is the set of all boys and sports playing girls.
The Venn diagram is as shown below.
The shaded areas represent the set A⋃(B⋂C)
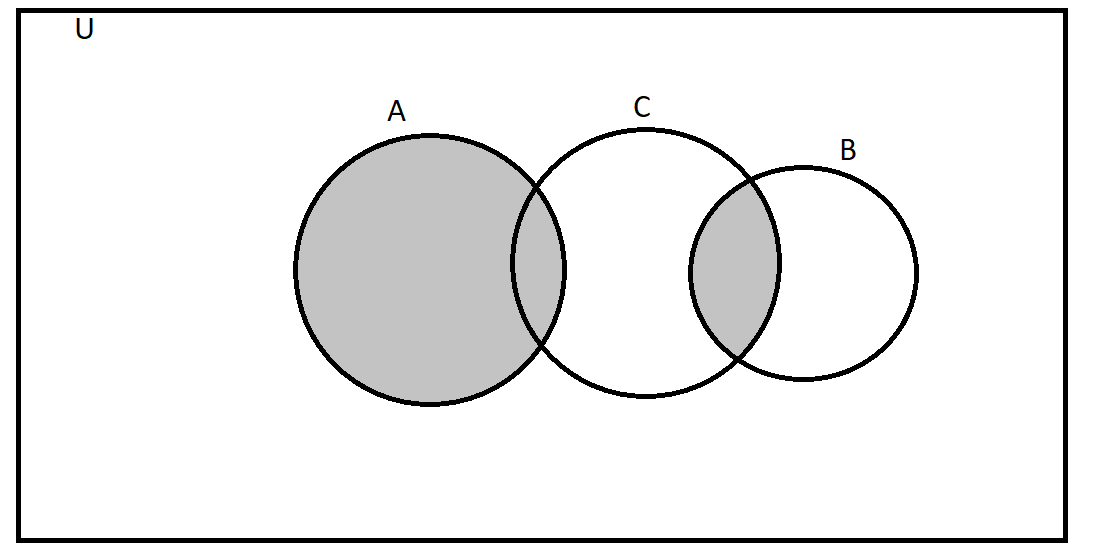
]
Note: The construction of the Venn diagram was sequential.
We first visualise what A looks like and what B⋂C looks like.
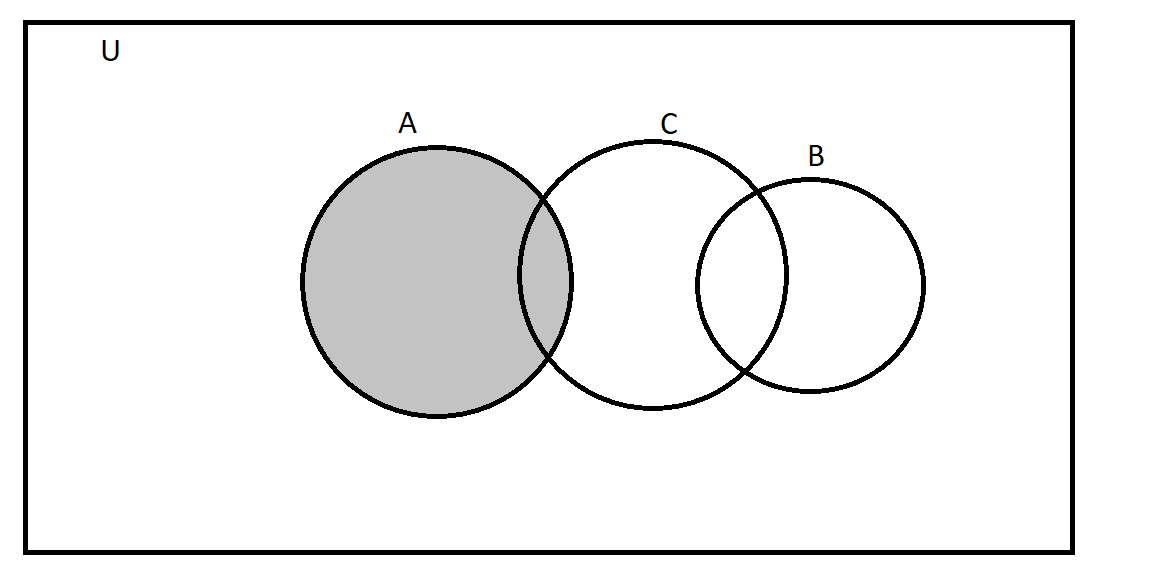
The shaded area is the set A.
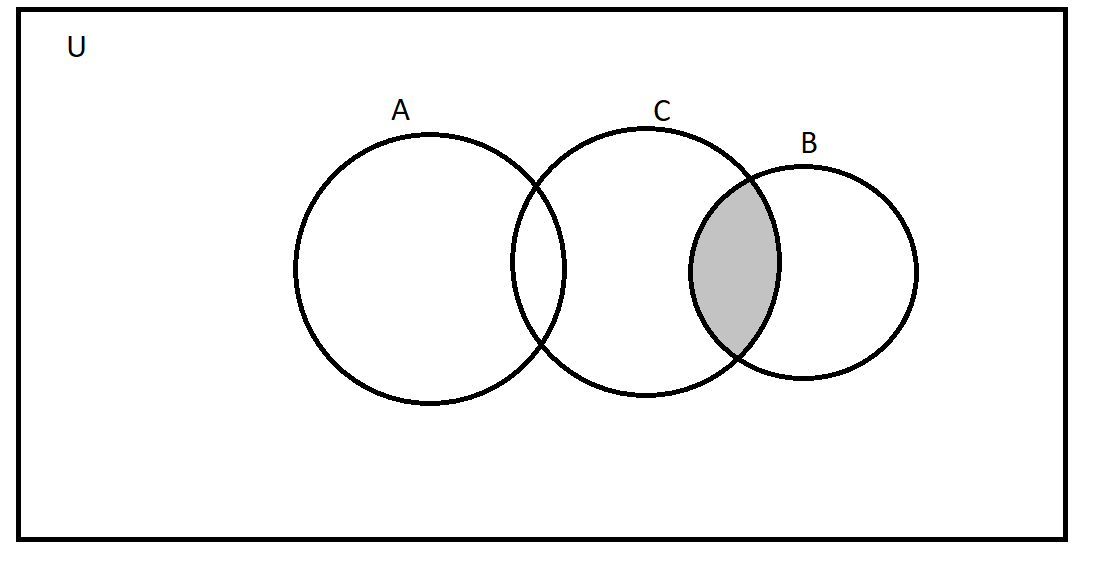
The shaded area is B⋂C.
Hence the Venn diagram of A⋃(B⋂C) is