Question

Let $U$ be the universal set and $A \cup B \cup C = U$. Then \left\\{ {\left( {A - B} \right) \cup \left( {B - C} \right) \cup \left( {C - A} \right)} \right\\}' is equal to
A.$A \cup B \cup C$
B.$A \cup \left( {B \cap C} \right)$
C.$A \cap B \cap C$
D.$A \cap \left( {B \cup C} \right)$

Answer 1

In order to find the value of \left\\{ {\left( {A - B} \right) \cup \left( {B - C} \right) \cup \left( {C - A} \right)} \right\\}', initiate with the drawing the Venn diagram of sets separately like for $\left( {A - B} \right)$, $\left( {B - C} \right)$ and $\left( {C - A} \right)$, find their union and then complement them. Complement will represent the part which is not covered by the unions. And, we will get the required results.

Complete answer:
We are given with three sets: A, B and C. And, some set equations are given, so we will use Venn diagrams to solve for \left\\{ {\left( {A - B} \right) \cup \left( {B - C} \right) \cup \left( {C - A} \right)} \right\\}'.
So, basically, we are given with $A \cup B \cup C = U$. Means all the elements of the sets combine to form the Universal set, which in diagram is represented as:

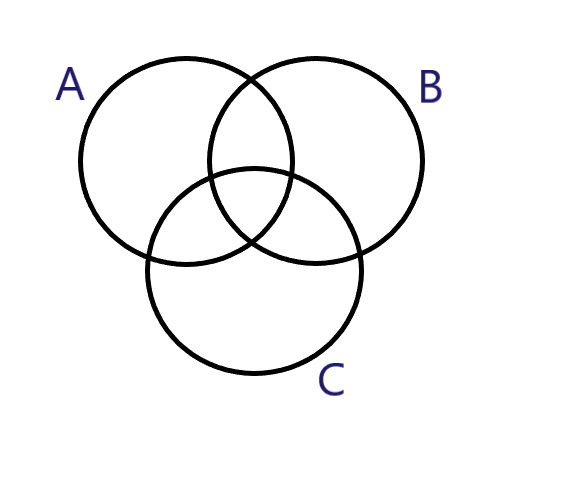
Now, we would start with finding the values separately in \left\\{ {\left( {A - B} \right) \cup \left( {B - C} \right) \cup \left( {C - A} \right)} \right\\}',.
Starting with $\left( {A - B} \right)$. Basically, $\left( {A - B} \right)$ it depicts the region which has all A elements except the portion which has B elements, represented as:

The Yellow portion shows $\left( {A - B} \right)$.
Now, for $\left( {B - C} \right)$, the Area’s which covers all elements of B but not C.
The pink color represents that:

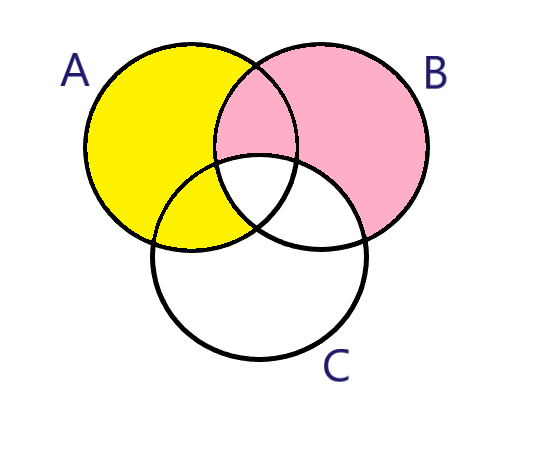
And, it gives $\left( {A - B} \right) \cup \left( {B - C} \right)$.
Now, for $\left( {C - A} \right)$.
The Area which has all elements of C but not the elements of A. Represented as green color:

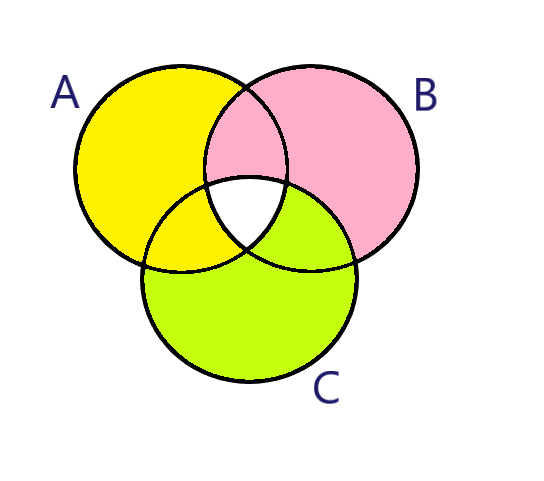
And, now it gives \left\\{ {\left( {A - B} \right) \cup \left( {B - C} \right) \cup \left( {C - A} \right)} \right\\}.
But we need the complement of the value. Complement means the portion which are in Universal set but not in \left\\{ {\left( {A - B} \right) \cup \left( {B - C} \right) \cup \left( {C - A} \right)} \right\\}.
So, the portion becomes:
\left\\{ {\left( {A - B} \right) \cup \left( {B - C} \right) \cup \left( {C - A} \right)} \right\\}' = U - \left\\{ {\left( {A - B} \right) \cup \left( {B - C} \right) \cup \left( {C - A} \right)} \right\\}
And, in the above diagram it is the white portion in the middle, which shows that. And, the portion is $A \cap B \cap C$, the intersection of the three sets.
Therefore, \left\\{ {\left( {A - B} \right) \cup \left( {B - C} \right) \cup \left( {C - A} \right)} \right\\}' is equal to $A \cap B \cap C$.
Therefore, option (C) is the correct answer.

Note:
-Universal sets are always represented by capital U. And, complement is represented with a single quote, for example: A’ is the complement of A.
-Venn Diagram is the best method to find the intersection and union of sets. So, it is always preferred to use Venn diagrams.