Question

Let two parallel lines $L_1$ and $L_2$ with positive slope are tangent to the circle $C_1 : x^2 + y^2 - 2x - 16y + 64 = 0$. If $L_1$ is also tangent to the circle $C_2 : x^2 + y^2 - 2x + 2y - 2 = 0$, $L_2$ doesn't meet $C_2$ at all and the equation of $L_2$ is $a\sqrt{a}x - by + c - a\sqrt{a} = 0$ where $a, b, c \in N$, then the minimum value of $\frac{a+b+c}{2}$ is equal to

Answer 1

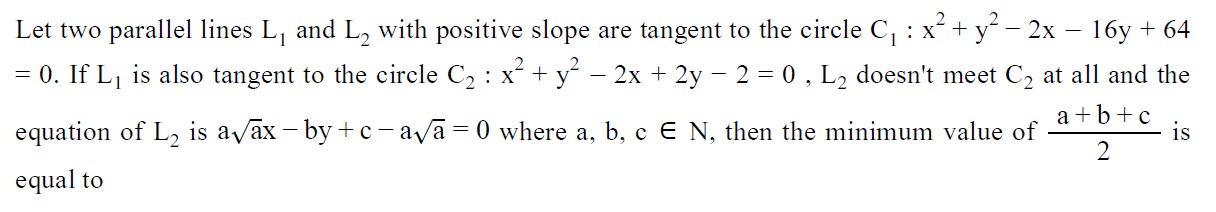
7

Answer 2

The equation of circle $C_1$ is $x^2 + y^2 - 2x - 16y + 64 = 0$. Completing the square, we get $(x^2 - 2x + 1) + (y^2 - 16y + 64) = 1$. So, $(x-1)^2 + (y-8)^2 = 1^2$. The center of $C_1$ is $O_1 = (1, 8)$ and its radius is $R_1 = 1.

The equation of circle $C_2$ is $x^2 + y^2 - 2x + 2y - 2 = 0$. Completing the square, we get $(x^2 - 2x + 1) + (y^2 + 2y + 1) = 2 + 1 + 1$. So, $(x-1)^2 + (y+1)^2 = 4$. The center of $C_2$ is $O_2 = (1, -1)$ and its radius is $R_2 = 2$.

Let the equation of the parallel lines $L_1$ and $L_2$ be $y = mx + k$, or $mx - y + k = 0$. Since the slope is positive, $m > 0$.

The distance from the center $O_1(1, 8)$ to the line $mx - y + k = 0$ must be equal to the radius $R_1 = 1$. $\frac{|m(1) - 8 + k|}{\sqrt{m^2 + (-1)^2}} = 1$ $|m - 8 + k| = \sqrt{m^2 + 1}$ This gives two possible values for $k$: $m - 8 + k = \sqrt{m^2 + 1} \implies k_A = 8 - m + \sqrt{m^2 + 1}$ $m - 8 + k = -\sqrt{m^2 + 1} \implies k_B = 8 - m - \sqrt{m^2 + 1}$ So, the two lines are $L_A: mx - y + k_A = 0$ and $L_B: mx - y + k_B = 0$. One of these is $L_1$ and the other is $L_2$.

The distance from the center $O_2(1, -1)$ to $L_1$ must be equal to the radius $R_2 = 2$. $\frac{|m(1) - (-1) + k_1|}{\sqrt{m^2 + 1}} = 2$ $|m + 1 + k_1| = 2\sqrt{m^2 + 1}$

Case 1: $L_1$ is $L_A$, so $k_1 = k_A = 8 - m + \sqrt{m^2 + 1}$. Substitute $k_A$ into the tangency condition for $C_2$: $|m + 1 + (8 - m + \sqrt{m^2 + 1})| = 2\sqrt{m^2 + 1}$ $|9 + \sqrt{m^2 + 1}| = 2\sqrt{m^2 + 1}$ Since $9 + \sqrt{m^2 + 1}$ is always positive, we can remove the absolute value: $9 + \sqrt{m^2 + 1} = 2\sqrt{m^2 + 1}$ $9 = \sqrt{m^2 + 1}$ Squaring both sides: $81 = m^2 + 1 \implies m^2 = 80$. Since $m > 0$, $m = \sqrt{80} = 4\sqrt{5}$. Now, find $k_A$ and $k_B$ with $m=4\sqrt{5}$: $\sqrt{m^2+1} = \sqrt{80+1} = \sqrt{81} = 9$. $k_A = 8 - 4\sqrt{5} + 9 = 17 - 4\sqrt{5}$. $k_B = 8 - 4\sqrt{5} - 9 = -1 - 4\sqrt{5}$. So, $L_1: 4\sqrt{5}x - y + (17 - 4\sqrt{5}) = 0$. And $L_2: 4\sqrt{5}x - y + (-1 - 4\sqrt{5}) = 0$.

Now, check the condition "$L_2$ doesn't meet $C_2$ at all". This means the distance from $O_2(1, -1)$ to $L_2$ must be greater than $R_2 = 2$. Distance $d(O_2, L_2) = \frac{|4\sqrt{5}(1) - (-1) + (-1 - 4\sqrt{5})|}{\sqrt{(4\sqrt{5})^2 + 1}} = \frac{|4\sqrt{5} + 1 - 1 - 4\sqrt{5}|}{\sqrt{80 + 1}} = \frac{|0|}{9} = 0$. Since $d(O_2, L_2) = 0 < R_2 = 2$, $L_2$ passes through the center of $C_2$, meaning it intersects $C_2$ at two points. This contradicts the condition that $L_2$ does not meet $C_2$. So, this case is invalid.

Case 2: $L_1$ is $L_B$, so $k_1 = k_B = 8 - m - \sqrt{m^2 + 1}$. Substitute $k_B$ into the tangency condition for $C_2$: $|m + 1 + (8 - m - \sqrt{m^2 + 1})| = 2\sqrt{m^2 + 1}$ $|9 - \sqrt{m^2 + 1}| = 2\sqrt{m^2 + 1}$ This equation has two possibilities: Subcase 2a: $9 - \sqrt{m^2 + 1} = 2\sqrt{m^2 + 1}$ (if $9 - \sqrt{m^2 + 1} \ge 0$) $9 = 3\sqrt{m^2 + 1}$ $3 = \sqrt{m^2 + 1}$ Squaring both sides: $9 = m^2 + 1 \implies m^2 = 8$. Since $m > 0$, $m = \sqrt{8} = 2\sqrt{2}$. Check the condition $9 - \sqrt{m^2 + 1} \ge 0$: $9 - \sqrt{8+1} = 9 - \sqrt{9} = 9 - 3 = 6 \ge 0$. This is consistent. So $m = 2\sqrt{2}$ is a valid slope. Now, find $k_A$ and $k_B$ with $m=2\sqrt{2}$: $\sqrt{m^2+1} = \sqrt{8+1} = \sqrt{9} = 3$. $k_B = 8 - 2\sqrt{2} - 3 = 5 - 2\sqrt{2}$. $k_A = 8 - 2\sqrt{2} + 3 = 11 - 2\sqrt{2}$. So, $L_1: 2\sqrt{2}x - y + (5 - 2\sqrt{2}) = 0$. And $L_2: 2\sqrt{2}x - y + (11 - 2\sqrt{2}) = 0$.

Now, check the condition "$L_2$ doesn't meet $C_2$ at all". Distance $d(O_2, L_2) = \frac{|2\sqrt{2}(1) - (-1) + (11 - 2\sqrt{2})|}{\sqrt{(2\sqrt{2})^2 + 1}} = \frac{|2\sqrt{2} + 1 + 11 - 2\sqrt{2}|}{\sqrt{8 + 1}} = \frac{|12|}{\sqrt{9}} = \frac{12}{3} = 4$. Since $d(O_2, L_2) = 4 > R_2 = 2$, $L_2$ does not meet $C_2$. This condition is satisfied. This is the correct set of lines.

Subcase 2b: $9 - \sqrt{m^2 + 1} = -2\sqrt{m^2 + 1}$ (if $9 - \sqrt{m^2 + 1} < 0$) $9 = -\sqrt{m^2 + 1}$ This is impossible because $\sqrt{m^2 + 1}$ is always positive, so $-\sqrt{m^2 + 1}$ is always negative. A positive number (9) cannot be equal to a negative number. No solution from this subcase.

The equation of $L_2$ is $2\sqrt{2}x - y + (11 - 2\sqrt{2}) = 0$. The given form of $L_2$ is $a\sqrt{a}x - by + c - a\sqrt{a} = 0$, where $a, b, c \in N$. Comparing the coefficients:

1. $a\sqrt{a} = 2\sqrt{2}$
2. $-b = -1 \implies b = 1$
3. $c - a\sqrt{a} = 11 - 2\sqrt{2}$

From (1), $a\sqrt{a} = 2\sqrt{2}$. Since $a \in N$, we can test values. If $a=1$, $1\sqrt{1}=1$. If $a=2$, $2\sqrt{2}$. This matches. So, $a=2$. From (2), $b=1$. This is a natural number. Substitute $a=2$ into (3): $c - 2\sqrt{2} = 11 - 2\sqrt{2}$ $c = 11$. This is a natural number.

We have $a=2, b=1, c=11$. All are natural numbers. We need to find the minimum value of $\frac{a+b+c}{2}$. Since we found unique values for $a, b, c$, this will be the only value. $\frac{a+b+c}{2} = \frac{2+1+11}{2} = \frac{14}{2} = 7$