Solveeit Logo
Login

Question

Question: Let three points A (2, 3, 4) B (3, 4, 2) and C (4, 2, 3) in space are given. A point D in space is s...

Let three points A (2, 3, 4) B (3, 4, 2) and C (4, 2, 3) in space are given. A point D in space is such that it is at a distance of 6\sqrt 6 units from 3 given points. Then volume of tetrahedron ABCD is:
A) 1
B) 3\sqrt 3
C) 13\sqrt {13}
D) 2

Explanation

Solution

Hint : Given the point D is equidistant from all points A, B and C. So the distance AD=BD=CD=6\sqrt 6 units. So using this find the coordinates of D. To calculate the volume of tetrahedron find the absolute value of the triple product and divide it by 6.

Complete step-by-step answer :

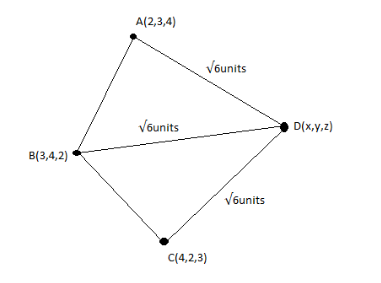
We are given that three points A (2, 3, 4) B (3, 4, 2) and C (4, 2, 3) are in space and a point D in space is equidistant from A, B, C and the distance between D and these three points is 6\sqrt 6 units.
Therefore, AD=BD=CD=6\sqrt 6 units.
Distance between two points with three coordinates x, y, z is (x2−x1)2+(y2−y1)2+(z2−z1)2\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{z_2} - {z_1}} \right)}^2}}
Let the coordinates of D be (x, y, z)
AD=BD
(2−x)2+(3−y)2+(4−z)2=(3−x)2+(4−y)2+(2−z)2\sqrt {{{\left( {2 - x} \right)}^2} + {{\left( {3 - y} \right)}^2} + {{\left( {4 - z} \right)}^2}} = \sqrt {{{\left( {3 - x} \right)}^2} + {{\left( {4 - y} \right)}^2} + {{\left( {2 - z} \right)}^2}}
Cancel the square root on both sides.
(2−x)2+(3−y)2+(4−z)2=(3−x)2+(4−y)2+(2−z)2 4−4x+x2+9−6y+y2+16−8z+z2=9−6x+x2+16−8y+y2+4−4z+z2 \-4x−6y−8z=−6x−8y−4z 4x+6y+8z=6x+8y+4z 2x+3y+4z=3x+4y+2z x+y=2z  {\left( {2 - x} \right)^2} + {\left( {3 - y} \right)^2} + {\left( {4 - z} \right)^2} = {\left( {3 - x} \right)^2} + {\left( {4 - y} \right)^2} + {\left( {2 - z} \right)^2} \\\ 4 - 4x + {x^2} + 9 - 6y + {y^2} + 16 - 8z + {z^2} = 9 - 6x + {x^2} + 16 - 8y + {y^2} + 4 - 4z + {z^2} \\\ \- 4x - 6y - 8z = - 6x - 8y - 4z \\\ 4x + 6y + 8z = 6x + 8y + 4z \\\ 2x + 3y + 4z = 3x + 4y + 2z \\\ x + y = 2z \\\
BD=CD
(3−x)2+(4−y)2+(2−z)2=(4−x)2+(2−y)2+(3−z)2\sqrt {{{\left( {3 - x} \right)}^2} + {{\left( {4 - y} \right)}^2} + {{\left( {2 - z} \right)}^2}} = \sqrt {{{\left( {4 - x} \right)}^2} + {{\left( {2 - y} \right)}^2} + {{\left( {3 - z} \right)}^2}}
Cancel the square root on both sides.
(3−x)2+(4−y)2+(2−z)2=(4−x)2+(2−y)2+(3−z)2 9−6x+x2+16−8y+y2+4−4z+z2=16−8x+x2+4−4y+y2+9−6z+z2 \-6x−8y−4z=−8x−4y−6z 6x+8y+4z=8x+4y+6z 3x+4y+2z=4x+2y+3z x+z=2y  {\left( {3 - x} \right)^2} + {\left( {4 - y} \right)^2} + {\left( {2 - z} \right)^2} = {\left( {4 - x} \right)^2} + {\left( {2 - y} \right)^2} + {\left( {3 - z} \right)^2} \\\ 9 - 6x + {x^2} + 16 - 8y + {y^2} + 4 - 4z + {z^2} = 16 - 8x + {x^2} + 4 - 4y + {y^2} + 9 - 6z + {z^2} \\\ \- 6x - 8y - 4z = - 8x - 4y - 6z \\\ 6x + 8y + 4z = 8x + 4y + 6z \\\ 3x + 4y + 2z = 4x + 2y + 3z \\\ x + z = 2y \\\
AD=CD
(2−x)2+(3−y)2+(4−z)2=(4−x)2+(2−y)2+(3−z)2\sqrt {{{\left( {2 - x} \right)}^2} + {{\left( {3 - y} \right)}^2} + {{\left( {4 - z} \right)}^2}} = \sqrt {{{\left( {4 - x} \right)}^2} + {{\left( {2 - y} \right)}^2} + {{\left( {3 - z} \right)}^2}}
Cancel the square root on both sides.

(2−x)2+(3−y)2+(4−z)2=(4−x)2+(2−y)2+(3−z)2 4−4x+x2+9−6y+y2+16−8z+z2=16−8x+x2+4−4y+y2+9−6z+z2 \-4x−6y−8z=−8x−4y−6z 4x+6y+8z=8x+4y+6z 2x+3y+4z=4x+2y+3z y+z=2y  {\left( {2 - x} \right)^2} + {\left( {3 - y} \right)^2} + {\left( {4 - z} \right)^2} = {\left( {4 - x} \right)^2} + {\left( {2 - y} \right)^2} + {\left( {3 - z} \right)^2} \\\ 4 - 4x + {x^2} + 9 - 6y + {y^2} + 16 - 8z + {z^2} = 16 - 8x + {x^2} + 4 - 4y + {y^2} + 9 - 6z + {z^2} \\\ \- 4x - 6y - 8z = - 8x - 4y - 6z \\\ 4x + 6y + 8z = 8x + 4y + 6z \\\ 2x + 3y + 4z = 4x + 2y + 3z \\\ y + z = 2y \\\

x+y=2z x+z=2y y+z=2x  x + y = 2z \\\ x + z = 2y \\\ y + z = 2x \\\
Solving the above equations we get D(x, y, z) = (2, 2, 2)
A(2, 3, 4), B(3, 4, 2), C(4, 2, 3), D(2, 2, 2) form a tetrahedron.
Volume of tetrahedron ABCD is \dfrac{1}{6}\left| {\begin{array}{*{20}{c}} {{u_1}}&{{u_2}}&{{u_3}} \\\ {{v_1}}&{{v_2}}&{{v_3}} \\\ {{w_1}}&{{w_2}}&{{w_3}} \end{array}} \right|

(u1,u2,u3)=(1,1,−2) (v1,v2,v3)=(2,−1,−1) (w1,w2,w3)=(0,−1,−2)  \left( {{u_1},{u_2},{u_3}} \right) = \left( {1,1, - 2} \right) \\\ \left( {{v_1},{v_2},{v_3}} \right) = \left( {2, - 1, - 1} \right) \\\ \left( {{w_1},{w_2},{w_3}} \right) = \left( {0, - 1, - 2} \right) \\\

Volume of the tetrahedron is \dfrac{1}{6}\left| {\begin{array}{*{20}{c}} {{u_1}}&{{u_2}}&{{u_3}} \\\ {{v_1}}&{{v_2}}&{{v_3}} \\\ {{w_1}}&{{w_2}}&{{w_3}} \end{array}} \right|

= \dfrac{1}{6}\left| {\begin{array}{*{20}{c}} 1&1&{ - 2} \\\ 2&{ - 1}&{ - 1} \\\ 0&{ - 1}&{ - 2} \end{array}} \right| \\\ = \dfrac{1}{6}\left[ {1 - \left( { - 4} \right) - 2\left( { - 2} \right)} \right] \\\ = \dfrac{1}{6}\left( {4 + 4 + 4} \right) \\\ = \dfrac{{12}}{6} = 2 \\\

Volume of the tetrahedron is 2 cube units, Option D is correct.
So, the correct answer is “Option D”.

Note : In geometry, a tetrahedron also known as a triangular pyramid is a polyhedron with four triangular faces, six straight edges, and four vertices. Prism and Pyramids of Egypt are examples of tetrahedrons.