Question
Question: Let the vectors **a**, **b**, **c** and **d** be such that \(( \mathbf { a } \times \mathbf { b } ) ...
Let the vectors a, b, c and d be such that (a×b)×(c×d)=0. Let P1 and P2 be planes determined by pair of vectors a,b and c,d respectively. Then the angle between P1 and P2 is
A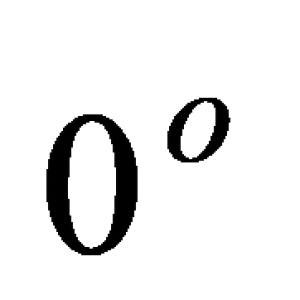
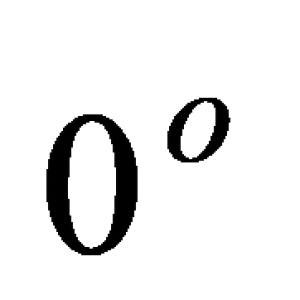
B
4π
C
3π
D
2π
Answer
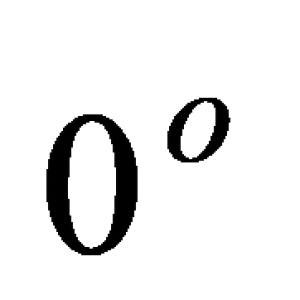
Explanation
Solution
(a×b)×(c×d)=0 ̃  is parallel to
is parallel to 
Hence plane P1 , determined by vectors a,b is parallel to the plane P2 determined by c,d
∴ Angle between P1 and P2 = 0 (As the planes P1 and P2 are parallel).
