Solveeit Logo
Login

Question

Question: Let the tangents PA and PB are drawn from P(0,-2) to the circle \({{x}^{2}}+{{y}^{2}}+2x-4y=0\). The...

Let the tangents PA and PB are drawn from P(0,-2) to the circle x2+y2+2x−4y=0{{x}^{2}}+{{y}^{2}}+2x-4y=0. The area of the triangle PAB is
[a] 21517\dfrac{2\sqrt{15}}{17}
[b] 41517\dfrac{4\sqrt{15}}{\sqrt{17}}
[c] 241517\dfrac{24\sqrt{15}}{17}
[d] 241517\dfrac{24\sqrt{15}}{\sqrt{17}}

Explanation

Solution

Use the fact that the equation of the chord of contact of tangents of the circle x2+y2+2gx+2fy+c=0{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0 from the point P(x1,y1)P\left( {{x}_{1}},{{y}_{1}} \right) is given by xx1+yy1+g(x+x1)+f(y+y1)+c=0x{{x}_{1}}+y{{y}_{1}}+g\left( x+{{x}_{1}} \right)+f\left( y+{{y}_{1}} \right)+c=0. Solve the equation of the chord of contact and the circle and hence find the coordinates of A and B. Use the fact that the area of the triangle formed by the points A(x1,y1),B(x2,y2),C(x3,y3)A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right),C\left( {{x}_{3}},{{y}_{3}} \right) is given by Δ=12∣x1y11 x2y21 x3y31 ∣\Delta =\dfrac{1}{2}\left| \begin{matrix} {{x}_{1}} & {{y}_{1}} & 1 \\\ {{x}_{2}} & {{y}_{2}} & 1 \\\ {{x}_{3}} & {{y}_{3}} & 1 \\\ \end{matrix} \right|
. Hence find the area of the triangle PAB.

Complete step by step answer:

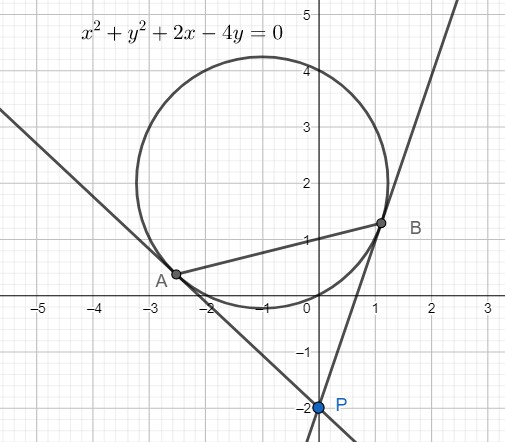
Equation of the circle is x2+y2+2x−4y=0{{x}^{2}}+{{y}^{2}}+2x-4y=0
We know that the equation of the chord of contact of the tangents of the circle x2+y2+2gx+2fy+c=0{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0 from the point P(x1,y1)P\left( {{x}_{1}},{{y}_{1}} \right) is given by xx1+yy1+(x+x1)+f(y+y1)+c=0x{{x}_{1}}+y{{y}_{1}}+\left( x+{{x}_{1}} \right)+f\left( y+{{y}_{1}} \right)+c=0
Hence the equation of AB is
x(0)+y(−2)+(x+0)−2(y−2)=0 x−4y+4=0 ⇒x=4y−4 \begin{aligned} & x\left( 0 \right)+y\left( -2 \right)+\left( x+0 \right)-2\left( y-2 \right)=0 \\\ & x-4y+4=0 \\\ & \Rightarrow x=4y-4 \\\ \end{aligned}
Substituting the value of x in the equation of the circle, we get
(4y−4)2+y2+2(4y−4)−4y=0 ⇒16y2+16−32y+y2+8y−8−4y=0 ⇒17y2−28y+8=0 \begin{aligned} & {{\left( 4y-4 \right)}^{2}}+{{y}^{2}}+2\left( 4y-4 \right)-4y=0 \\\ & \Rightarrow 16{{y}^{2}}+16-32y+{{y}^{2}}+8y-8-4y=0 \\\ & \Rightarrow 17{{y}^{2}}-28y+8=0 \\\ \end{aligned}
Let the roots of this expression be y1,y2{{y}_{1}},{{y}_{2}}
Hence, we have y1+y2=2817,y1y2=817{{y}_{1}}+{{y}_{2}}=\dfrac{28}{17},{{y}_{1}}{{y}_{2}}=\dfrac{8}{17}
Also, we have A≡(4y1−4,y1),B≡(4y2−4,y2)A\equiv \left( 4{{y}_{1}}-4,{{y}_{1}} \right),B\equiv \left( 4{{y}_{2}}-4,{{y}_{2}} \right)
We know that the area of the triangle ΔABC\Delta ABC formed by the points A(x,1,y1),B(x2,y2),C(x3,y3)A\left( {{x}_{,1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right),C\left( {{x}_{3}},{{y}_{3}} \right) is given by Δ=12∣x1y11 x2y21 x3y31 ∣\Delta =\dfrac{1}{2}\left| \begin{matrix} {{x}_{1}} & {{y}_{1}} & 1 \\\ {{x}_{2}} & {{y}_{2}} & 1 \\\ {{x}_{3}} & {{y}_{3}} & 1 \\\ \end{matrix} \right| which we expand by row operations and third column to have Δ=12∣x2−x1y2−y1 x3−x1y3−y1 ∣\Delta =\dfrac{1}{2}\left| \begin{matrix} {{x}_{2}}-{{x}_{1}} & {{y}_{2}}-{{y}_{1}} \\\ {{x}_{3}}-{{x}_{1}} & {{y}_{3}}-{{y}_{1}} \\\ \end{matrix} \right|
Hence, we have
ar(ΔPAB)=12∣4y1−4−0y1+2 4y2−4−0y2+2 ∣ar\left( \Delta PAB \right)=\dfrac{1}{2}\left| \begin{matrix} 4{{y}_{1}}-4-0 & {{y}_{1}}+2 \\\ 4{{y}_{2}}-4-0 & {{y}_{2}}+2 \\\ \end{matrix} \right|
Hence, we have
ar(ΔPAB)=12∣(4y1−4)(y2+2)−(4y2−4)(y1+2)∣ar\left( \Delta PAB \right)=\dfrac{1}{2}\left| \left( 4{{y}_{1}}-4 \right)\left( {{y}_{2}}+2 \right)-\left( 4{{y}_{2}}-4 \right)\left( {{y}_{1}}+2 \right) \right|
Taking 4 common inside modulus sign, we get
ar(ΔPAB)=2∣(y1−1)(y2+2)−(y2−1)(y1+2)∣ar\left( \Delta PAB \right)=2\left| \left( {{y}_{1}}-1 \right)\left( {{y}_{2}}+2 \right)-\left( {{y}_{2}}-1 \right)\left( {{y}_{1}}+2 \right) \right|
Expanding the terms inside the modulus sign, we get
ar(ΔPAB)=2∣y1y2+2y1−y2−2−y1y2−2y2+y1+2∣ =6∣y1−y2∣ \begin{aligned} & ar\left( \Delta PAB \right)=2\left| {{y}_{1}}{{y}_{2}}+2{{y}_{1}}-{{y}_{2}}-2-{{y}_{1}}{{y}_{2}}-2{{y}_{2}}+{{y}_{1}}+2 \right| \\\ & =6\left| {{y}_{1}}-{{y}_{2}} \right| \\\ \end{aligned}
We know that (a−b)2=(a+b)2−4ab{{\left( a-b \right)}^{2}}={{\left( a+b \right)}^{2}}-4ab
Hence, we have
(y1−y2)2=(y1+y2)2−4y1y2=282172−3217=282−17×32172=240172{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}={{\left( {{y}_{1}}+{{y}_{2}} \right)}^{2}}-4{{y}_{1}}{{y}_{2}}=\dfrac{{{28}^{2}}}{{{17}^{2}}}-\dfrac{32}{17}=\dfrac{{{28}^{2}}-17\times 32}{{{17}^{2}}}=\dfrac{240}{{{17}^{2}}}
Taking square root on both sides, we get
∣y1−y2∣=41517\left| {{y}_{1}}-{{y}_{2}} \right|=\dfrac{4\sqrt{15}}{17}
Hence, we have
ar(ΔPAB)=6(41517)=241517ar\left( \Delta PAB \right)=6\left( \dfrac{4\sqrt{15}}{17} \right)=\dfrac{24\sqrt{15}}{17}

So, the correct answer is “Option c”.

Note: [1] This question can also be solved directly using Pythagoras theorem and trigonometry without the use of analytical geometry. However the calculations will be more tedious to perform. Hence the method should be avoided as it is more prone to calculation mistakes.