Question
Question: Let the tangent at point P of the curve \({{x}^{2m}}{{y}^{\dfrac{n}{2}}}={{a}^{\dfrac{4m+n}{2}}}\) m...
Let the tangent at point P of the curve x2my2n=a24m+n meets the x-axis and the y-axis at A and B, respectively. If AP:PB=λmn, where P lies between A and B, then find the value of λ
[a] 4
[b] 3
[c] -4
[d] -3
Solution
Take logarithm on both sides of the equation and differentiate with respect to x, Hence find the expression for dxdy. Hence find the slope of the tangent at a point P(x1,y1) on the given curve and hence find the equation of the tangent. Determine the coordinates of points of intersection of the tangent with the axis. Hence determine the ratio in which P divides AB.
Alternatively form the equation of the family of the curves whose tangent at point P meets x-axis at A and B and satisfies AP: PB =λmn. Solve the differential equation and compare with the given equation. Hence find the value of λ.
Complete step-by-step answer:
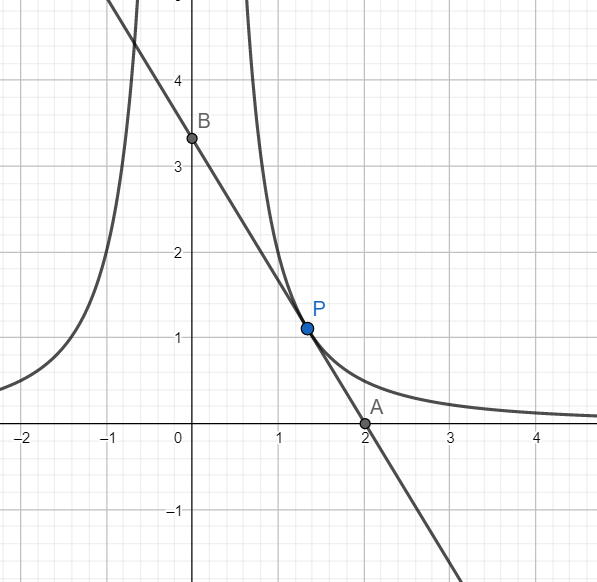
We have x2my2n=a24m+n
Taking log on both sides, we get
logx2my2n=loga24m+n
Using logmn=logm+logn and log(an)=nloga, we get
2mlogx+2nlogy=24m+nloga
Differentiating both sides of the equation, we get
2mx1+2ny1dxdy=0
Subtracting x2m from both sides of the equation, we get
2yndxdy=x−2m
Multiplying both sides of the equation by n2y, we get
dxdy=nx−4my
Hence the slope of the tangent at P(x1,y1) is given by m=dxdyx=x1,y=y1=nx1−4my1
Hence the equation of the tangent is given by
y−y1=nx1−4my1(x−x1)
At point A, we have y = 0
Hence, we have
−y1=nx1−4my1(x−x1)⇒nx1=4m(x−x1)
Dividing both sides by 4m, we get
x−x1=4mnx1
Adding x1 on both sides, we get
x=4mn+4mx1
At point B, we have x=0.
Hence, we have
y−y1=nx1−4my1(−x1)=n4my1
Adding y1 on both sides of the equation, we get
y=(n4m+1)y1=n4m+ny1
Let P divides AB in the ratio of k:1
Hence, we have
P≡k+1k×0+4m4m+nx1,k+1k×n4m+ny1
But P≡(x1,y1)
Hence, we have
4m(k+1)4m+n=1
Multiplying both sides by k+1, we get
k+1=4m4m+n
Subtracting 1 from both sides, we get
k=4m4m+n−1=4mn
Hence the ratio in which P divides AB is 4mn
Hence λ=4
Hence option [a] is correct
So, the correct answer is “Option [a]”.
Note: Alternative Method: Best method
Equation of the tangent at point P(x,y) is given by
Y−y=dxdy(X−x)
At point A, we have Y = 0
Hence −y=dxdy(X−x)
Hence, we have
X=x+dxdy−y
Since P divides AB in the ratio λmn, we have
x=n+λmλmx−dxdyy
Multiplying both sides by n+λm, we get
(n+λm)x=λmx−dxdyy
Dividing both sides byλm , we get
λmn+λmx=x−dxdyy
Subtracting x from both sides, we get
λmnx=−dxdyy⇒λmnx=−ydydx⇒ydy=−nλmxdx
Integrating both sides, we get
logy=−nλmlogx+logC
Hence, we have
logyxnλm=logC
Hence, we have
yxnλm=C
Raising power to 2n on both sides of the equation, we get
y2nx2λm=C2n=C′
Comparing the equation, with the given equation, we get
2λ=2⇒λ=4
Hence, the value of λ is 4
