Question

Let the Straight line $x{\text{ }} = b$ divide the area enclosed by $y = {\text{ }}{\left( {1 - x} \right)^2},{\text{ }}y{\text{ }} = {\text{ }}0,{\text{ }}$ and ${\text{ }}x{\text{ }} = {\text{ }}0$ into two parts ${R_1}$ ($0 \leqslant x \leqslant b$) and ${R_2}$ ($b \leqslant x \leqslant 1$) such that ${R_1} - {R_2} = \dfrac{1}{4}$. Then $b$ equals
A) $\dfrac{3}{4}$
B) $\dfrac{1}{2}$
C) $\dfrac{1}{3}$
D) $\dfrac{1}{4}$

Answer 1

In this question, the equation of parabola is given and a straight line is intersecting it, so, we have to find the area of the shaded region. We will use integration to solve this question. It will consider being easy if we plot and look forward to what we want to determine.

Complete step-by-step answer:
It is given that the area enclosed by the given equation (Parabola) is $y = {(1 - x)^2}$ and $x{\text{ }} = {\text{ }}b$ is a straight line and also $x{\text{ }} = 0{\text{ }}$ and ${\text{ }}y{\text{ }} = {\text{ }}0$.
So, according to the question, diagram is as follows:

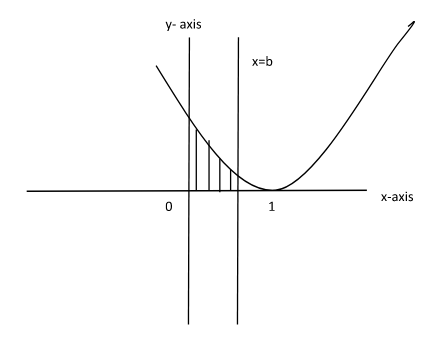
Description of the above diagram is as follows:
Since,
$x{\text{ }} = {\text{ }}b$ is the equation of line.
We have to find the area of the shaded region which is enclosed by the line and upwards parabola.
So, first we need to determine the area of the shaded region which can be determined as follows
Area of shaded region = $\int\limits_0^1 {{{\left( {1 - x} \right)}^2}} - 0dx$
Here, ${R_1}$ ($0 \leqslant x \leqslant b$)
In above it is written that the value of x varies from $0$ to $b$
Or
In simple words it means that limit goes from $0$ to $b$
$R_1 = \int\limits_0^1 {{{\left( {1 - x} \right)}^2}} dx$
Integrating the above integral, we get
$= \left. {\dfrac{{{{(1 - x)}^{2 + 1}}}}{{2 + 1}} \times - 1} \right|_0^b$
Simplifying the above integral
$\left. { = \dfrac{{ - {{(1 - x)}^3}}}{3}} \right|_0^b$
Now,
Similarly, we will find the value of $R_2$
${R_2}$ $(b \leqslant x \leqslant 1)$, It means that limit will go from $b$ to $1$.
$R_2 = \int\limits_b^1 {{{\left( {1 - x} \right)}^2}dx}$
Integrating the above integral, we get
$= \left. {\dfrac{{{{(1 - x)}^{2 + 1}}}}{{2 + 1}} \times - 1} \right|_0^1$
Simplifying the above integral, we get
$= \left. {\dfrac{{ - {{(1 - x)}^3}}}{3}} \right|_b^1$
Limit varies from $b$ to $1$
${R_1} - {R_2} = \dfrac{1}{4}$
Substituting the value of ${R_1}$ and ${R_2}$, we get
$= \dfrac{{ - {{(1 - b)}^3}}}{3} + \dfrac{1}{3} - \dfrac{{{{(1 - b)}^3}}}{3} = \dfrac{1}{4}$
Simplifying the above, we get
$= \dfrac{{ - 2}}{3}{(1 - b)^3} = \dfrac{1}{4} - \dfrac{1}{3}$
Taking least common factor in the right hand limit, After simplification we get
$= \dfrac{{ - 2}}{3}{(1 - b)^3} = - \dfrac{1}{{12}}$
On simplifying for $b$, we get
$= {(1 - b)^3} = - \dfrac{1}{{12}} \times \dfrac{{ - 3}}{2} = \dfrac{1}{8}$
$\Rightarrow 1 - b = \dfrac{1}{2}$
So, the required value of $b$ comes out to be
$\Rightarrow b = \dfrac{1}{2}$

$\therefore$ The value of b is equal to $\dfrac{1}{2}$. Hence, option (B) is correct.

Note: Parabola is symmetric about its own axis. The axis of the parabola will be perpendicular to the directrix. The axis of the parabola passes through the vertex and the focus. The tangent at the vertex of the parabola is parallel to the directrix.