Question

Let the sets A and B be A=\left\\{ 1,2,3,4,5,6 \right\\},B=\left\\{ 2,4,6,8,10 \right\\}. Verify that
$A\Delta B=\left( A-B \right)\cup \left( B-A \right)=\left( A\cup B \right)-\left( A\cap B \right)$ where $A\Delta B$ is the symmetric difference of A and B.

Answer 1

To solve this question, we should know the symmetric difference of A and B. The symmetric difference of two sets A and B is defined as the set of elements which are either in A or in B but not in both the sets. The above formula can be proved using the venn diagrams but we are asked to show it using the given sets A and B. We know the definition of $A-B$ as the elements which are present only in A but not in B. Using this we can calculate the L.H.S. We know the definitions of $A\cup B$ and $A\cap B$ as the set of all the elements combining the elements of A and B and the set of all the elements which are common in A and B respectively. We can calculate the R.H.S and prove that L.H.S is equal to R.H.S.

Complete step by step answer:
We are given two sets A and B which are
A=\left\\{ 1,2,3,4,5,6 \right\\},B=\left\\{ 2,4,6,8,10 \right\\}
We should prove the equation $A\Delta B=\left( A-B \right)\cup \left( B-A \right)=\left( A\cup B \right)-\left( A\cap B \right)$.
Let us first calculate the values of $A-B$, $B-A$,$A\cup B$ and $A\cap B$
We know the definition of $A-B$ as the elements which are present only in A but not in B.
Mathematically we can write it as
$A-B=A-\left( A\cap B \right)$
Let us consider $A-B$ in the given sets. The set$A\cap B$ is the common elements in both the sets which are
A\cap B=\left\\{ 2,4,6 \right\\}
So, we can write that
\begin{aligned} & A-B=A-\left\\{ 2,4,6 \right\\}=\left\\{ 1,2,3,4,5,6 \right\\}-\left\\{ 2,4,6 \right\\}=\left\\{ 1,3,5 \right\\} \\\ & A-B=\left\\{ 1,3,5 \right\\} \\\ \end{aligned}
Let us consider $B-A$.
\begin{aligned} & B-A=B-\left( A\cap B \right) \\\ & B-A=\left\\{ 2,4,6,8,10 \right\\}-\left\\{ 2,4,6 \right\\}=\left\\{ 8,10 \right\\} \\\ \end{aligned}
Let us calculate $A\cup B$. It is the set of all the elements combined in the sets A and B.
A\cup B=\left\\{ 1,2,3,4,5,6 \right\\}\cup \left\\{ 2,4,6,8,10 \right\\}=\left\\{ 1,2,3,4,5,6,8,10 \right\\}
Let us consider the L.H.S of the required equation which is $\left( A-B \right)\cup \left( B-A \right)$
By using the calculated sets in the above expression, we get
\left( A-B \right)\cup \left( B-A \right)=\left\\{ 1,3,5 \right\\}\cup \left\\{ 8,10 \right\\}=\left\\{ 1,3,5,8,10 \right\\}
Let us consider the R.H.S of the equation which is $\left( A\cup B \right)-\left( A\cap B \right)$
Using the derived values, we get
\left( A\cup B \right)-\left( A\cap B \right)=\left\\{ 1,2,3,4,5,6,8,10 \right\\}-\left\\{ 2,4,6 \right\\}=\left\\{ 1,3,5,8,10 \right\\}
We got the relation as
$A\Delta B=\left( A-B \right)\cup \left( B-A \right)=\left( A\cup B \right)-\left( A\cap B \right)$
Hence proved.

Note: We can also use the venn diagrams to understand the symmetric difference of two sets. Let us consider two sets A and B. The symmetric difference is given by the below shaded region

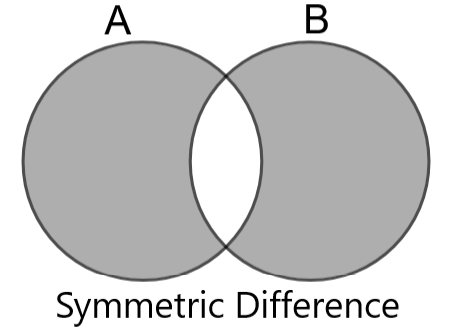
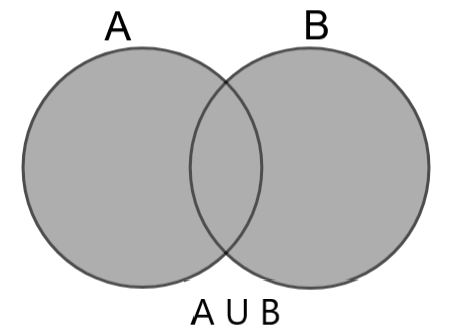
The set $A\cup B$ is shown in the venn diagram by the shaded area

The set $A\cap B$ is shown by the venn diagram

We can clearly see from the above diagrams that we can get the first figure if we subtract the third figure from the second one. Likewise, we can prove the other equation also.