Question

Let the population of honey-bees surviving at a time is given by the differential equation $\frac{dx}{dt} = \frac{1}{2}x + 50$, if $x(0) = 200$, then $x(t)$ is equal to $ae^{t/2} - b$. The value of $a - b$ is

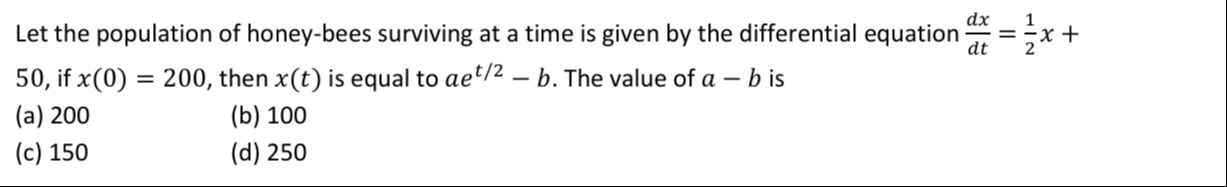
• A. 200
• B. 100
• C. 150
• D. 250

Answer 1

Answer: (A)

200

Answer 2

The given differential equation is $\frac{dx}{dt} = \frac{1}{2}x + 50$.
This is a first-order separable differential equation. We can rewrite it as:
$\frac{dx}{\frac{1}{2}x + 50} = dt$

Integrate both sides:
$\int \frac{dx}{\frac{1}{2}x + 50} = \int dt$

To integrate the left side, let $u = \frac{1}{2}x + 50$. Then $du = \frac{1}{2} dx$, which means $dx = 2 du$.
$\int \frac{2 du}{u} = \int dt$
$2 \int \frac{du}{u} = \int dt$
$2 \ln|u| = t + C_1$, where $C_1$ is the constant of integration.
Substitute back $u = \frac{1}{2}x + 50$:
$2 \ln|\frac{1}{2}x + 50| = t + C_1$
$\ln|\frac{1}{2}x + 50| = \frac{t}{2} + \frac{C_1}{2}$
$|\frac{1}{2}x + 50| = e^{\frac{t}{2} + \frac{C_1}{2}} = e^{C_1/2} e^{t/2}$
$\frac{1}{2}x + 50 = A e^{t/2}$, where $A = \pm e^{C_1/2}$ is an arbitrary constant.

Now, solve for $x(t)$:
$\frac{1}{2}x = A e^{t/2} - 50$
$x(t) = 2A e^{t/2} - 100$

We are given the initial condition $x(0) = 200$. Substitute $t=0$ and $x=200$ into the equation:
$200 = 2A e^{0/2} - 100$
$200 = 2A e^0 - 100$
$200 = 2A(1) - 100$
$200 = 2A - 100$
$2A = 200 + 100$
$2A = 300$
$A = 150$

Substitute the value of $A$ back into the solution for $x(t)$:
$x(t) = 2(150) e^{t/2} - 100$
$x(t) = 300 e^{t/2} - 100$

The problem states that $x(t)$ is equal to $ae^{t/2} - b$.
Comparing our solution $x(t) = 300 e^{t/2} - 100$ with the given form $x(t) = ae^{t/2} - b$, we can identify the values of $a$ and $b$:
$a = 300$
$b = 100$

We are asked to find the value of $a - b$.
$a - b = 300 - 100 = 200$.