Solveeit Logo
Login

Question

Question: Let the opposite angular points of a square be (3, 4) and (1, – 1). Find the coordinates of the rema...

Let the opposite angular points of a square be (3, 4) and (1, – 1). Find the coordinates of the remaining angular points.

Explanation

Solution

Hint: In this question, first of all, draw the square ABCD, and take A (3, 4), B (x, y), and C (1, – 1). Now equate the sides AB and BC by using the distance formula (x2−x1)2+(y2−y1)2\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}. Then apply Pythagoras theorem in ΔABC\Delta ABC that is AB2+BC2=AC2A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}. From solving these two equations, get the values of x and y.

Complete step-by-step answer:
Here, we are given that opposite angular points of a square be (3, 4) and (1, – 1). We have to find the coordinates of the remaining angular points. First of all, let us consider a square ABCD in which coordinates of points A and C are (3, 4) and (1, – 1) respectively. Also, let us assume the coordinates of point B as (x, y).

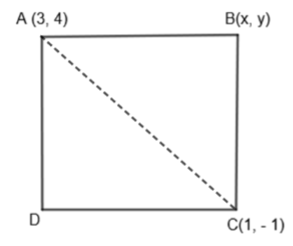
We know that all the sides of the square are equal. So, let us equate the sides AB and BC.
AB = BC
We know that the distance between two points can be calculated by using the distance formula given as:
d=(x2−x1)2+(y2−y1)2.....(i)d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}.....\left( i \right)
So, we get,
AB=(x−3)2+(y−4)2AB=\sqrt{{{\left( x-3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}}
And we get,
BC=(x−1)2+(y+1)2BC=\sqrt{{{\left( x-1 \right)}^{2}}+{{\left( y+1 \right)}^{2}}}
By substituting the values of AB and BC in equation (i), we get,
(x−3)2+(y−4)2=(x−1)2+(y+1)2\sqrt{{{\left( x-3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}}=\sqrt{{{\left( x-1 \right)}^{2}}+{{\left( y+1 \right)}^{2}}}
By squaring both the sides of the above equation, we get,
(x−3)2+(y−4)2=(x−1)2+(y+1)2{{\left( x-3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}={{\left( x-1 \right)}^{2}}+{{\left( y+1 \right)}^{2}}
We know that, (a+b)2=a2+b2+2ab{{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab and (a−b)2=a2+b2−2ab{{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab. By using these, we get,
⇒x2+9−6x+y2+16−8y=x2+1−2x+y2+1+2y\Rightarrow {{x}^{2}}+9-6x+{{y}^{2}}+16-8y={{x}^{2}}+1-2x+{{y}^{2}}+1+2y
By canceling the like terms and transferring all the terms to LHS, we get,
9−6x+16−8y−1+2x−1−2y=09-6x+16-8y-1+2x-1-2y=0
⇒−4x−10y+23=0\Rightarrow -4x-10y+23=0
x=23−10y4....(ii)x=\dfrac{23-10y}{4}....\left( ii \right)
Also, in right angle triangle ABC, by using the Pythagoras theorem, we get,
(AB)2+(BC)2=(AC)2{{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}={{\left( AC \right)}^{2}}
By distance formula, we get AB, BC, and AC as,
((x−3)2+(y−4)2)2+((x−1)2+(y+1)2)2=((3−1)2+(4+1)2)2{{\left( \sqrt{{{\left( x-3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}} \right)}^{2}}+{{\left( \sqrt{{{\left( x-1 \right)}^{2}}+{{\left( y+1 \right)}^{2}}} \right)}^{2}}={{\left( \sqrt{{{\left( 3-1 \right)}^{2}}+{{\left( 4+1 \right)}^{2}}} \right)}^{2}}
(x−3)2+(y−4)2+(x−1)2+(y+1)2=(2)2+(5)2{{\left( x-3 \right)}^{2}}+{{\left( y-4 \right)}^{2}}+{{\left( x-1 \right)}^{2}}+{{\left( y+1 \right)}^{2}}={{\left( 2 \right)}^{2}}+{{\left( 5 \right)}^{2}}
x2+9−6x+y2+16−8y+x2+1−2x+y2+1+2y=4+25{{x}^{2}}+9-6x+{{y}^{2}}+16-8y+{{x}^{2}}+1-2x+{{y}^{2}}+1+2y=4+25
⇒2x2+2y2−8x−6y−2=0\Rightarrow 2{{x}^{2}}+2{{y}^{2}}-8x-6y-2=0
By dividing the whole equation by 2, we get,
x2+y2−4x−3y−1=0{{x}^{2}}+{{y}^{2}}-4x-3y-1=0
By substituting the value of x from equation (ii), we get,
(23−10y4)2+y2−4(23−10y4)−3y−1=0{{\left( \dfrac{23-10y}{4} \right)}^{2}}+{{y}^{2}}-4\left( \dfrac{23-10y}{4} \right)-3y-1=0
⇒(23−10y4)2+y2−(23−10y)−3y−1=0\Rightarrow {{\left( \dfrac{23-10y}{4} \right)}^{2}}+{{y}^{2}}-\left( 23-10y \right)-3y-1=0
(23−10y)216+y2−23+10y−3y−1=0\dfrac{{{\left( 23-10y \right)}^{2}}}{16}+{{y}^{2}}-23+10y-3y-1=0
(529+100y2−460y)16+y2+7y−24=0\dfrac{\left( 529+100{{y}^{2}}-460y \right)}{16}+{{y}^{2}}+7y-24=0
By multiplying 16 on both sides of the above equation, we get,
529+100y2−460y+16y2+112y−384=0529+100{{y}^{2}}-460y+16{{y}^{2}}+112y-384=0
By simplifying the above equation, we get,
116y2−348y+145=0116{{y}^{2}}-348y+145=0
By dividing the whole equation by 29, we get,
4y2−12y+5=04{{y}^{2}}-12y+5=0
⇒4y2−10y−2y+5=0\Rightarrow 4{{y}^{2}}-10y-2y+5=0
2y(2y−5)−1(2y−5)=02y\left( 2y-5 \right)-1\left( 2y-5 \right)=0
By taking out (2y – 5) common, we get,
(2y−5)(2y−1)=0\left( 2y-5 \right)\left( 2y-1 \right)=0
So, we get, y=52,12y=\dfrac{5}{2},\dfrac{1}{2}.
By substituting y=52y=\dfrac{5}{2} and y=12y=\dfrac{1}{2} in equation (ii), we get,
x=23−10(52)4=−12x=\dfrac{23-10\left( \dfrac{5}{2} \right)}{4}=\dfrac{-1}{2}
And, x=23−10(12)4=92x=\dfrac{23-10\left( \dfrac{1}{2} \right)}{4}=\dfrac{9}{2}
Hence, we get the coordinates of B and D as (−12,52)\left( \dfrac{-1}{2},\dfrac{5}{2} \right) and (92,12)\left( \dfrac{9}{2},\dfrac{1}{2} \right).

Note: In this question, some students assume point D as the variable and try to solve the equation in 4 variables which gets very lengthy. So, they must note that the sequence is one of the most symmetrical to each other as well. So, we need not take the coordinates of B and D individually because they are symmetrical with respect to the other two points and whatever that is true for B would be true for D as well and vice- versa.