Question

Let the line $\dfrac{{x - 2}}{3} = \dfrac{{y - 1}}{{ - 5}} = \dfrac{{z + 2}}{2}$ lie in the plane$x + 3y - \alpha z + \beta = 0$, then $\left( {\alpha ,\beta } \right)$ equals
${\text{A}}{\text{. }}\left( {7, - 7} \right) \\\ {\text{B}}{\text{. }}\left( { - 6,7} \right) \\\ {\text{C}}{\text{. }}\left( {2, - 16} \right) \\\ {\text{D}}{\text{. }}\left( { - 6,6} \right) \\\$

Answer 1

Here we go through by the properties of the plane and the properties of the line. As we know that if the direction ratio of the plane is the same as the line perpendicular to the plane. So we apply dot product for solving this question.

Complete step-by-step answer :
Here in the question it is given that the line $\dfrac{{x - 2}}{3} = \dfrac{{y - 1}}{{ - 5}} = \dfrac{{z + 2}}{2}$ lie in the plane$x + 3y - \alpha z + \beta = 0$.
First of all we have to make a rough diagram showing the equation of line and plane and then shows the direction ratios of it.
And as we know that the direction ratios of the plane defines that the direction ratio of the line which is perpendicular to the plane. We also show this in our diagram.

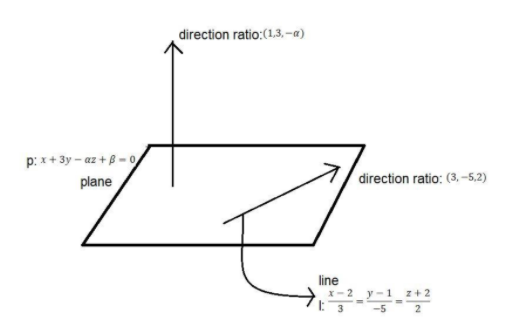
As from the figure we can say that the point contained in the line should also lie on the plane.
And the point which the line contains is found by equating the equation of line by zero. We get,
$\dfrac{{x - 2}}{3} = \dfrac{{y - 1}}{{ - 5}} = \dfrac{{z + 2}}{2} = 0$
Therefore the points that lie on the lines are x=2, y=1 and z=-2.
And from the figure the line is on the plane so these points should also lie on the plane so we put the value of these points on the equation of the plane. We get,
$\Rightarrow 2 + 3 \times 1 - \alpha ( - 2) + \beta = 0$
$\Rightarrow 2\alpha + \beta = - 5$ Let it as equation (I)
And we know that the direction ratio of normal to the plane i.e. $1,3, - \alpha$ and the direction ratio of the line i.e. 3,-5, 2.
And we know that the given line is perpendicular to the normal of the plane because it lies on the plane.
So the dot product of the direction ratios are zero.
i.e. $\Rightarrow 3 \times 1 + 3 \times ( - 5) + ( - \alpha ) \times 2 = 0$
$\Rightarrow 2\alpha = - 12 \\\ \therefore \alpha = - 6 \\\$
Now put the value of $\alpha$in equation (I) we get,
$\Rightarrow - 12 + \beta = - 5 \\\ \Rightarrow \beta = - 5 + 12 = 7 \\\$
$\therefore \left( {\alpha ,\beta } \right) = \left( { - 6,7} \right)$
Hence, option 'B' is the correct answer.

Note : Whenever we face such a type of question the key concept for solving the question is first of all find the direction ratios of the given line and the direction ratios of normal to the plane. And then satisfy the point that lies on the line on the plane to make an equation and for other equations make a dot product between two direction ratios.