Question

Let the length of the latus rectum of an ellipse with its major axis along $x$ -axis and centre at the origin be 8. If the distance between the foci of this ellipse is equal to the length of its minor axis, then one of the following points lie on it?
(a) $\left( 4\sqrt{3},2\sqrt{3} \right)$
(b) $\left( 4\sqrt{3},2\sqrt{2} \right)$
(c) $\left( 4\sqrt{2},2\sqrt{2} \right)$
(d) $\left( 4\sqrt{2},2\sqrt{3} \right)$

Answer 1

We will first let a general form of the equation of ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$
And with the help of given conditions and properties of an ellipse we will find the value of the constants in the equation of ellipse. Once we get to know the equation , we can check which option lies on the ellipse, keeping in mind that if the point satisfies the equation of the ellipse then it lies on it.

Complete step-by-step answer:
First , we will draw an ellipse with the equation $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ , showing its latus rectum , vertex ,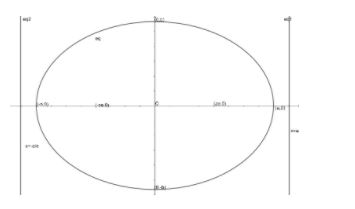

Now, we will use the given conditions to get more information about this ellipse,
For the ellipse,
$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$
We know that the length of latus rectum is equal to- $\dfrac{2{{b}^{2}}}{a}$
And we are given the question that it is equal to 8.
$\Rightarrow \dfrac{2{{b}^{2}}}{a}=8$
and
$\begin{aligned} & 2ae=2b \\\ & \Rightarrow e=\dfrac{b}{a} \\\ & \Rightarrow 1-{{e}^{2}}={{e}^{2}} \\\ & \Rightarrow 2{{e}^{2}}=1 \\\ & \Rightarrow e=\dfrac{1}{\sqrt{2}} \\\ & \Rightarrow b=4\sqrt{2} \\\ & \Rightarrow a=8 \\\ \end{aligned}$
Since, we have the values of $a$ and $b$ , we can get the equation of ellipse by it, i.e.
$\begin{aligned} & \dfrac{{{x}^{2}}}{{{8}^{2}}}+\dfrac{{{y}^{2}}}{4{{\sqrt{2}}^{2}}}=1 \\\ & \Rightarrow \dfrac{{{x}^{2}}}{64}+\dfrac{{{y}^{2}}}{32}=1 \\\ \end{aligned}$
Now, since we have the equation of ellipse now, we can find the point from the options which is passing through it,
For option (a),
$\begin{aligned} & \left( 4\sqrt{3},2\sqrt{3} \right) \\\ & \dfrac{{{\left( 4\sqrt{3} \right)}^{2}}}{64}+\dfrac{{{\left( 2\sqrt{3} \right)}^{2}}}{32} \\\ & =\dfrac{48}{64}+\dfrac{12}{32} \\\ & =\dfrac{9}{8}\ne 1 \\\ \end{aligned}$
Hence, option (a) is not correct.
For option (b),
$\begin{aligned} & \left( 4\sqrt{3},2\sqrt{2} \right) \\\ & \dfrac{{{\left( 4\sqrt{3} \right)}^{2}}}{64}+\dfrac{{{\left( 2\sqrt{2} \right)}^{2}}}{32} \\\ & =\dfrac{48}{64}+\dfrac{8}{32} \\\ & =\dfrac{64}{64}=1 \\\ \end{aligned}$
Hence, $\left( 4\sqrt{3},2\sqrt{2} \right)$ satisfies the equation of the ellipse and hence it is the point which is lying on it.

So, the correct answer is “Option b”.

Note: The possibility of mistake here is while using the given conditions and properties of ellipse we can get confused with the use of $a$ and $b$ , so while using these conditions we have to remember that $x$ - axis is the major axis and $a$ is the $x$ - intercept and $b$ is the $y$ - intercept. And then using these conditions we are going to evaluate constants in the equation and will proceed the same.