Question

Let the ground state electronic energy of hydrogen atom be $E_H$ eV. The first excited state energy of deuterium atom (in eV) is

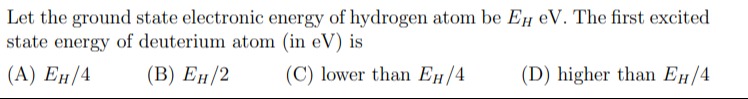
• A. $E_H/4$
• B. $E_H/2$
• C. lower than $E_H/4$
• D. higher than $E_H/4$

Answer 1

Answer: (C)

lower than $E_H/4$

Answer 2

The energy of an electron in a hydrogen-like atom is $E_n \propto -\frac{\mu}{n^2}$, where $\mu$ is the reduced mass. The reduced mass $\mu = \frac{m_e M}{m_e + M}$ increases with the nuclear mass $M$. Since the deuteron mass ($M_d$) is greater than the proton mass ($M_p$), the reduced mass for deuterium ($\mu_D$) is greater than that for hydrogen ($\mu_H$).

The ground state energy of hydrogen is $E_H = -\frac{\mu_H R_y^\infty}{m_e}$.

The first excited state energy of deuterium is $E_{D, n=2} = -\frac{\mu_D R_y^\infty}{4m_e}$.

Comparing $E_{D, n=2}$ with $E_H/4 = -\frac{\mu_H R_y^\infty}{4m_e}$.

Since $\mu_D > \mu_H$, it follows that $\frac{\mu_D}{4m_e} > \frac{\mu_H}{4m_e}$. Therefore, $-\frac{\mu_D R_y^\infty}{4m_e} < -\frac{\mu_H R_y^\infty}{4m_e}$, which means $E_{D, n=2}$ is lower than $E_H/4$.