Question

Let the function $f$ be defined by $f(x)=\frac{x^3(2\sec x -1)+\sec x(4x+2)-2x-1}{x+\alpha}$ for all permissible values of $x$. If $f(x)=0$ has no solution then $[\alpha]=$ ___ ([.] represents G.I.F)

Answer 1

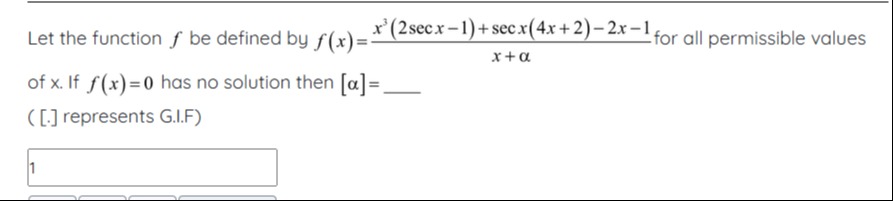
0

Answer 2

Let the given function be $f(x)=\frac{x^3(2\sec x -1)+\sec x(4x+2)-2x-1}{x+\alpha}$. We want to find the value of $[\alpha]$ such that the equation $f(x)=0$ has no solution.

First, let's simplify the numerator of $f(x)$. Let the numerator be $N(x)$. $N(x) = x^3(2\sec x -1)+\sec x(4x+2)-2x-1$ $N(x) = 2x^3\sec x - x^3 + 4x\sec x + 2\sec x - 2x - 1$

Grouping terms with $\sec x$ and terms without $\sec x$: $N(x) = (2x^3\sec x + 4x\sec x + 2\sec x) + (-x^3 - 2x - 1)$ $N(x) = \sec x (2x^3 + 4x + 2) - (x^3 + 2x + 1)$ $N(x) = 2\sec x (x^3 + 2x + 1) - (x^3 + 2x + 1)$

Factoring out the common term $(x^3 + 2x + 1)$: $N(x) = (2\sec x - 1)(x^3 + 2x + 1)$

The function $f(x)$ is defined as $f(x) = \frac{(2\sec x - 1)(x^3 + 2x + 1)}{x+\alpha}$. The permissible values of $x$ are those for which $\sec x$ is defined and the denominator is non-zero. $\sec x$ is defined when $\cos x \neq 0$, i.e., $x \neq \frac{\pi}{2} + n\pi$ for any integer $n$. The denominator is non-zero when $x+\alpha \neq 0$, i.e., $x \neq -\alpha$. So, the domain of $f(x)$ is $D = \{x \in \mathbb{R} \mid x \neq \frac{\pi}{2} + n\pi \text{ for any } n \in \mathbb{Z} \text{ and } x \neq -\alpha\}$.

The equation $f(x)=0$ is $\frac{(2\sec x - 1)(x^3 + 2x + 1)}{x+\alpha} = 0$. This equation is equivalent to $N(x)=0$ for $x$ in the domain $D$. $N(x)=0 \implies (2\sec x - 1)(x^3 + 2x + 1) = 0$. This equation holds if and only if $2\sec x - 1 = 0$ or $x^3 + 2x + 1 = 0$, provided $x \neq \frac{\pi}{2} + n\pi$.

Case 1: $2\sec x - 1 = 0$. $\sec x = \frac{1}{2}$. $\cos x = 2$. Since the range of $\cos x$ is $[-1, 1]$, the equation $\cos x = 2$ has no real solution. So, the factor $(2\sec x - 1)$ is never zero for any real $x$.

Case 2: $x^3 + 2x + 1 = 0$. Let $g(x) = x^3 + 2x + 1$. We need to find the real roots of this cubic equation. Let's analyze $g(x)$. The derivative is $g'(x) = 3x^2 + 2$. Since $x^2 \ge 0$, $3x^2 \ge 0$, so $g'(x) = 3x^2 + 2 \ge 2 > 0$ for all real $x$. Since $g'(x) > 0$, $g(x)$ is a strictly increasing function. A strictly increasing cubic function has exactly one real root. Let this unique real root be $x_0$. We can estimate the value of $x_0$ by checking some values: $g(-1) = (-1)^3 + 2(-1) + 1 = -1 - 2 + 1 = -2$. $g(0) = 0^3 + 2(0) + 1 = 1$. Since $g(-1) < 0$ and $g(0) > 0$, the root $x_0$ lies between -1 and 0. Let's try values between -1 and 0: $g(-0.5) = (-0.5)^3 + 2(-0.5) + 1 = -0.125 - 1 + 1 = -0.125$. $g(-0.4) = (-0.4)^3 + 2(-0.4) + 1 = -0.064 - 0.8 + 1 = 0.136$. Since $g(-0.5) < 0$ and $g(-0.4) > 0$, the root $x_0$ lies between -0.5 and -0.4. So, $-0.5 < x_0 < -0.4$.

The numerator $N(x)=(2\sec x - 1)(x^3 + 2x + 1)$ is zero if and only if $x^3 + 2x + 1 = 0$, provided $x \neq \frac{\pi}{2} + n\pi$. The only real value of $x$ that makes $x^3 + 2x + 1 = 0$ is $x_0$. We need to check if $x_0$ is of the form $\frac{\pi}{2} + n\pi$. The values $\frac{\pi}{2} + n\pi$ are approximately ..., $-4.71, -1.57, 1.57, 4.71, ...$. Since $-0.5 < x_0 < -0.4$, $x_0$ is not equal to $\frac{\pi}{2} + n\pi$ for any integer $n$. Thus, $x_0$ is a value where $\sec x_0$ is defined.

So, the equation $N(x)=0$ for $x \neq \frac{\pi}{2} + n\pi$ has exactly one solution, $x=x_0$.

The equation $f(x)=0$ is $\frac{N(x)}{x+\alpha}=0$. This equation has a solution if and only if there exists a value of $x$ in the domain $D$ such that $N(x)=0$. We found that $N(x)=0$ for $x \neq \frac{\pi}{2} + n\pi$ occurs only at $x=x_0$. The domain $D$ requires $x \neq \frac{\pi}{2} + n\pi$ (which $x_0$ satisfies) and $x \neq -\alpha$. So, the equation $f(x)=0$ has a solution if and only if $x_0$ is in the domain $D$. This means $x_0 \neq -\alpha$.

The problem states that $f(x)=0$ has no solution. This occurs if the only value of $x$ that makes the numerator zero is not in the domain of $f(x)$. The only real value of $x$ for which the numerator is zero (and $\sec x$ is defined) is $x_0$. $x_0$ is not of the form $\frac{\pi}{2} + n\pi$, so $\sec x_0$ is defined. The domain restriction that could exclude $x_0$ is $x \neq -\alpha$. Therefore, $f(x)=0$ has no solution if and only if $x_0 = -\alpha$. This means $\alpha = -x_0$.

We know that $-0.5 < x_0 < -0.4$. Multiplying the inequality by -1 and reversing the inequality signs, we get: $0.4 < -x_0 < 0.5$. Substituting $\alpha = -x_0$, we have: $0.4 < \alpha < 0.5$.

The question asks for $[\alpha]$, which is the greatest integer less than or equal to $\alpha$. Since $0.4 < \alpha < 0.5$, the greatest integer less than or equal to $\alpha$ is 0. $[\alpha] = 0$.