Question

Let the equation of the ellipse is $\frac{x^2}{16} + \frac{y^2}{4} = 1$. The largest circle having centre (1, 0) that can be inscribed in an ellipse has radius

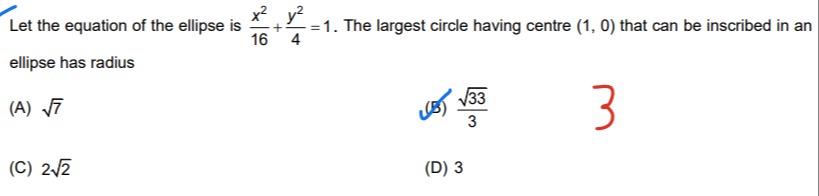
• A. $\sqrt{7}$
• B. $\frac{\sqrt{33}}{3}$
• C. $2\sqrt{2}$
• D. 3

Answer 1

Answer: (B)

$\frac{\sqrt{33}}{3}$

Answer 2

The largest inscribed circle with a given center inside an ellipse has a radius equal to the minimum distance from the center to the boundary of the ellipse.

Given ellipse: $\frac{x^2}{16} + \frac{y^2}{4} = 1$. Center of circle: (1, 0).

We minimize the squared distance $D^2 = (x-1)^2 + y^2$ subject to $\frac{x^2}{16} + \frac{y^2}{4} = 1$.

Substitute $y^2 = 4 - \frac{x^2}{4}$ from the ellipse equation into the squared distance formula:

$D^2(x) = (x-1)^2 + 4 - \frac{x^2}{4} = x^2 - 2x + 1 + 4 - \frac{x^2}{4} = \frac{3x^2}{4} - 2x + 5$.

This is a quadratic function of $x$. The minimum value occurs at $x = -\frac{-2}{2(3/4)} = \frac{4}{3}$.

The minimum squared distance is $D^2(\frac{4}{3}) = \frac{3}{4}(\frac{4}{3})^2 - 2(\frac{4}{3}) + 5 = \frac{3}{4} \cdot \frac{16}{9} - \frac{8}{3} + 5 = \frac{4}{3} - \frac{8}{3} + 5 = -\frac{4}{3} + 5 = \frac{11}{3}$.

The minimum distance is $\sqrt{\frac{11}{3}} = \frac{\sqrt{33}}{3}$.

This is the radius of the largest inscribed circle centered at (1, 0).