Question

Let the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ contains the circle $(x-1)^2+y^2=1$ and has least area. If $a^2+b^2=2n$, then find the value of $n \in N$.

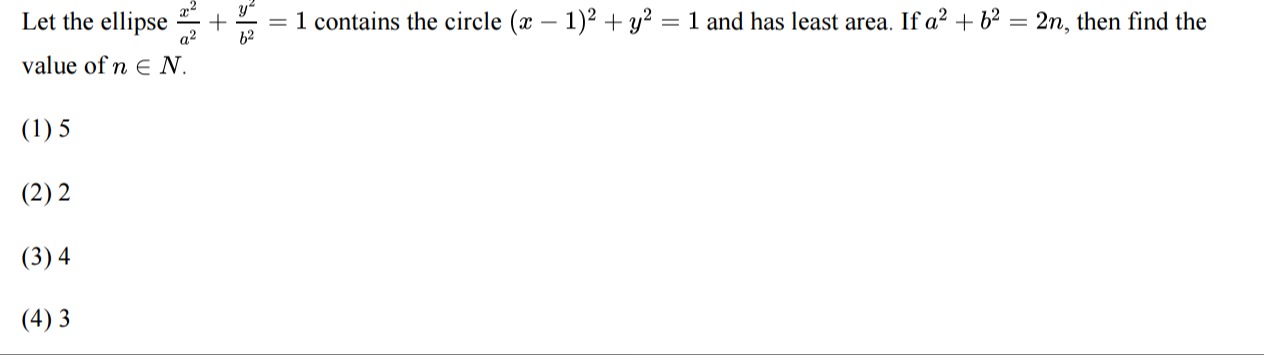
• A. 5
• B. 2
• C. 4
• D. 3

Answer 1

Answer: (D)

3

Answer 2

The ellipse is

$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,$$

and it must contain the circle

$$(x-1)^2+y^2=1.$$

For the ellipse of minimum area (i.e. minimum $\pi ab$) that contains the circle, the circle will be tangent to the ellipse. At the tangency point $(x,y)$ on the circle, we have

$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \quad \text{and} \quad (x-1)^2+y^2=1.$$

Using the method of Lagrange multipliers to maximize

$$f(x,y) = \frac{x^2}{a^2} + \frac{y^2}{b^2}$$

subject to

$$g(x,y) = (x-1)^2+y^2=1,$$

we obtain the conditions (for $y\ne0$):

$$\frac{2x}{a^2} - 2\lambda(x-1) = 0,\quad \frac{2y}{b^2} - 2\lambda y = 0.$$

For $y\ne 0$ the second equation gives $\lambda = \frac{1}{b^2}$. Plugging into the first gives:

$$\frac{x}{a^2} = \frac{x-1}{b^2} \quad \Longrightarrow \quad x = \frac{a^2}{a^2-b^2}.$$

Let $a^2=k$ and $b^2=d$ with $k>d$. Then the tangency condition and the circle’s equation lead (after some algebra) to the relation

$$d\,(k-d-1) = k-d.$$

Writing $D = k-d$ (with $D>0$) the equation becomes:

$$d\,(D-1) = D \quad \Longrightarrow \quad d = \frac{D}{D-1}.$$

Thus,

$$a^2 = k = D + d = D + \frac{D}{D-1} = \frac{D^2}{D-1}, \quad b^2 = \frac{D}{D-1}.$$

The ellipse’s area (ignoring $\pi$) is proportional to $ab = \sqrt{a^2b^2} = \frac{D\sqrt{D}}{D-1}$.

To minimize the area, differentiate $f(D)=\frac{D^{3/2}}{D-1}$ with respect to $D$. Calculating,

$$f'(D)= \frac{D^{1/2}[(D-1)(\frac{3}{2})-D]}{(D-1)^2}.$$

Setting the numerator to zero:

$$D^{1/2}\left[\frac{3}{2}(D-1)-D\right]=0 \quad \Longrightarrow \quad \frac{3}{2}(D-1)-D=0.$$

Solving,

$$\frac{3D-3-2D}{2}=0 \quad \Longrightarrow \quad D-3=0 \quad \Longrightarrow \quad D=3.$$

Substitute $D=3$ back:

$$a^2 = \frac{3^2}{3-1} = \frac{9}{2},\quad b^2 = \frac{3}{2}.$$

Thus,

$$a^2+b^2 = \frac{9}{2}+\frac{3}{2} = \frac{12}{2} = 6.$$

Since $a^2+b^2=2n$, we have:

$$2n=6 \quad \Longrightarrow \quad n=3.$$

Answer: Option (4) 3

---

Explanation (minimal):
Set up the tangency condition between the ellipse and circle using Lagrange multipliers. Derive $x=\frac{a^2}{a^2-b^2}$ and, after algebra, express $a^2$ and $b^2$ in terms of $D=a^2-b^2$. Minimize the area function $\frac{D^{3/2}}{D-1}$ with respect to $D$ and find $D=3$. This yields $a^2+b^2=6=2n$, so $n=3$.