Question

Let the dimensions of the rectangular plot of the greatest area be $length=l$and $breadth=b$which can be laid out within a triangle of $base\text{ }36ft.$ and $altitude\text{ }12ft$. Assume that one side of the rectangle lies on the base of the triangle. Find $\dfrac{l}{b}$ ?

Answer 1

For answering this question we will use the given information and draw a diagram and use the similarity property and derive a relation between $l$ and $b$. After that, as it is given it is the greatest rectangular plot so it will have the maximum area it means its first derivative will be zero and the second derivative will be negative. And extract a dimension and use it and derive the other dimension.

Complete step-by-step solution
Now considering from the question it is given that the dimensions of a triangle is base $36\text{ ft}\text{.}$ and altitude $12\text{ ft}\text{.}$ and the dimensions of the greatest rectangular plot that can be laid within the triangle is given as length $l\text{ ft}\text{.}$ and breadth $b\text{ f}t.$
So we can say that the area of the rectangle will be $lb$.

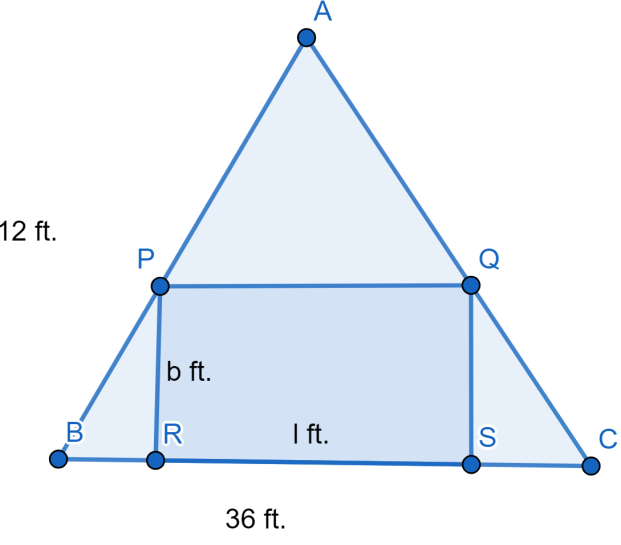
And by observing we can say that the triangles $\Delta ABC$ and $\Delta APQ$ are similar. We can say that the ratios of corresponding base and altitude will be equal which is mathematically given as $\dfrac{12-b}{12}=\dfrac{l}{36}$.
This gives us a simplified equation relating the length and breadth $\left( 12-b \right)36=12l\Rightarrow \left( 12-b \right)3=l$ .
By substituting this in the expression for the area we will have $b\left( 12-b \right)3$.
As it is given that the rectangular plot is greatest the area will be maximum which implies that its first derivative will be equal to zero which is mathematically given as $\dfrac{d}{dx}b\left( 12-b \right)3=0$.
For performing derivations we will use the formulae $\dfrac{d}{dx}uv=v\dfrac{d}{dx}u+u\dfrac{d}{dx}v$ .
After applying this formulae we will have
$\begin{aligned} & \dfrac{d}{dx}b\left( 12-b \right)3=0 \\\ & \Rightarrow 3\left( 12-b \right)\dfrac{d}{dx}b+3b\dfrac{d}{dx}\left( 12-b \right)=0 \\\ & \Rightarrow 3\left( 12-b \right)+3b\left( -1 \right)=0 \\\ & \Rightarrow \left( 36-3b \right)-3b=0 \\\ \end{aligned}$ .
By further simplifying this we will have $36-3b-3b=0\Rightarrow 36-6b=0\Rightarrow b=6\text{ ft}\text{.}$ .
And the second derivative of the expression should be negative at that point then only the rectangular plot will have a maximum area which can be given mathematically as $\dfrac{{{d}^{2}}}{d{{x}^{2}}}b\left( 12-b \right)3<0$.
By applying derivation here we will have
$\begin{aligned} & \dfrac{{{d}^{2}}}{d{{x}^{2}}}b\left( 12-b \right)3<0 \\\ & \Rightarrow \dfrac{d}{dx}\left[ 3\left( 12-b \right)+3b\left( -1 \right) \right]<0 \\\ & \Rightarrow \dfrac{d}{dx}\left[ 36-6b \right]<0 \\\ & \Rightarrow -6<0 \\\ \end{aligned}$
By using the value of $b$ in the equation $\left( 12-b \right)3=l$ we will have $l=3\left( 12-6 \right)=18\text{ ft}\text{.}$ .
Hence we can conclude that $\dfrac{l}{b}=3$.

Note: While answering questions of this type we should take care while observing the corresponding sides and applying derivative for the area. The general fact is that when a polynomial function has a maximum or minimum value its first derivative will be zero value and the second derivative will be negative for the maximum case and positive for the minimum case. The important point is the corresponding sides of similar objects will be in the same ratio.