Question

Let the curve $C$ be the mirror image of the parabola ${y^2} = 4x$ with respect to the line $x + y + 4 = 0$. If $A$ and $B$ are the points of intersection of $C$ with the line $y = - 5$ , then the distance between $A$ and $B$ is (units).

Answer 1

Here we are asked to find the distance between two points at the intersection of the given parabola with the given line. There could be two ways to solve this problem: first we calculate the equation of the curve $C$ then we calculate their intersection point with line $y = - 5$ and then we calculate the distance between $A$ and $B$ . And another way around we could do is calculate the mirror image of $y = - 5$ with respect to the line $x + y + 4 = 0$ and once we calculate the mirror image we can calculate the intersection point of the parabola and that mirror image and where ever they intersect we can just calculate the distance between those two points that would be equal to $A$ and $B$.
Formula: Formula that we need to know:
If there are two points $({x_1},{y_1}),({x_2},{y_2})$
Then the distance between them: $\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}}$

Complete answer:
This problem can be approached in two ways, the first way is calculating the equation of the curve $C$ and calculating their intersection point with line $y = - 5$ and then calculating the distance between $A$ and $B$ . The second way is calculating the mirror image of $y = - 5$ with respect to the line $x + y + 4 = 0$ then calculating the intersection point of the parabola and that mirror image then we can calculate the distance between those two point where ever they intersect.
So it's very obvious that if we try to take a mirror image of a linear equation that would be easier than if we try to get the mirror image of parabola so here we will choose the easiest way.
To get a clear idea of this problem refer to the above diagram.

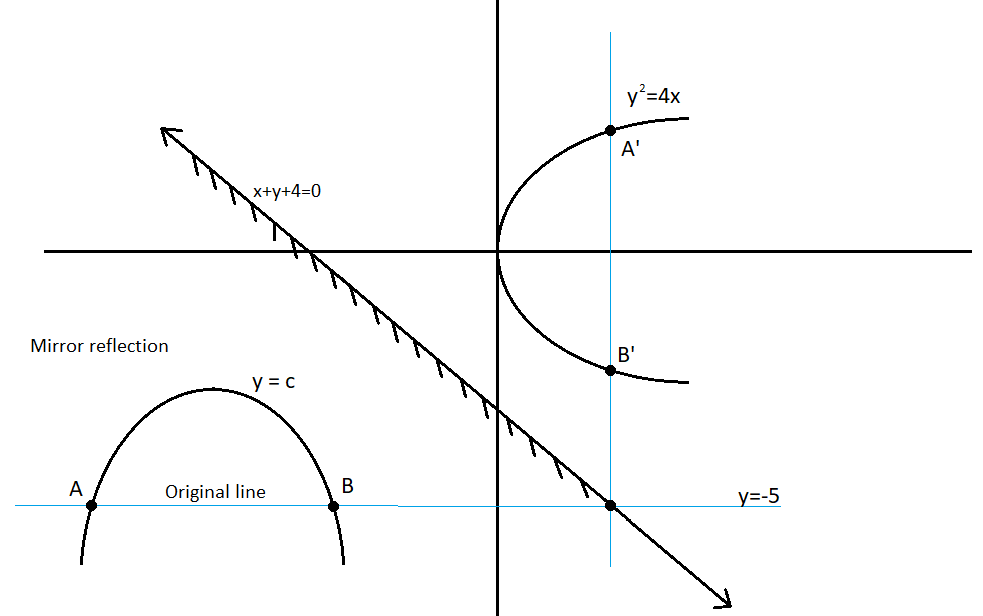
The mirror image $y = - 5$ in the line $x + y + 4 = 0$
To calculate the image line place the value of $y$ in the equation $x + y + 4 = 0$
$x + ( - 5) + 4 = 0$
$x - 1 = 0$
$x = 1$
So the image line will be $x = 1$
Now if we calculate the intersection point of line $x = 1$ with ${y^2} = 4x$
Place the value of $x$ in the parabola equation to find two points

$${y^2} = 4x \\\ {y^2} = 4(1) \\\ {y^2} = 4 \\\ y = \sqrt 4 \\\ y = \pm 2 \\\$$

Now we have two points that are $(1, - 2)$ and $(1,2)$
Now the distance between these two points would be equal to the distance between $A$ and $B$
According to the distance formula, distance between $A$ and $B$ can be calculated as

$$AB = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} \\\ AB = \sqrt {{{(1 - 1)}^2} + {{(2 - ( - 2))}^2}} \\\ AB = \sqrt {{{(0)}^2} + {{(4)}^2}} \\\ AB = \sqrt {{{(4)}^2}} \\\ AB = 4 \\\$$

Hence the distance between points $A$ and $B$ is $4$

Note:
Since there are two methods to solve this problem we crossed the easiest way and found the distance. When we put the value in the parabola equation we will get two values of $y$ hence there will be two intersection points. Students must be more attentive while doing simple calculations. The chances are high of committing mistakes in that.