Question

Let ${\text{f : [0,1] }} \to {\text{ R}}$(the set of all real numbers) be a function. Suppose the function f is twice differentiable, f(0) = f(1) = 0 and satisfies ${\text{f ''}}\left( {\text{x}} \right){\text{ - 2f '}}\left( {\text{x}} \right){\text{ + f}}\left( {\text{x}} \right) \geqslant {{\text{e}}^{\text{x}}}{\text{, x}} \in {\text{[0,1]}}$.
If the function ${e^{ - x}}.f\left( x \right)$ assumes its minimum in the interval [0,1] at $x = \dfrac{1}{4}$, which of the following is true?
${\text{A}}{\text{. f '(x) < f(x),}}\dfrac{1}{4} < x < \dfrac{3}{4} \\\ {\text{B}}{\text{. f '(x) > f(x),0}} < x < \dfrac{1}{4} \\\ {\text{C}}{\text{. f '(x) < f(x),0}} < x < \dfrac{1}{4} \\\ {\text{D}}{\text{. f '(x) < f(x),}}\dfrac{3}{4} < x < 1 \\\$

Answer 1

Multiply the expression ${\text{f ''}}\left( {\text{x}} \right){\text{ - 2f '}}\left( {\text{x}} \right){\text{ + f}}\left( {\text{x}} \right) \geqslant {{\text{e}}^{\text{x}}}$ by ${e^{ - x}}$ and then proceed with the calculations. Our main aim is to check the slope of f’(x) and compare it with f(x). In order to do that, find the concavity of the function obtained after certain calculative steps.

Complete step-by-step answer:
The given information about the function f(x) is that it is twice differentiable.
And f(0) = f(1) = 0
Also, ${\text{f ''}}\left( {\text{x}} \right){\text{ - 2f '}}\left( {\text{x}} \right){\text{ + f}}\left( {\text{x}} \right) \geqslant {{\text{e}}^{\text{x}}}{\text{, x}} \in {\text{[0,1]}}$
Multiply the above expression by${e^{ - x}}$. This gives us-

$${\text{f ''}}\left( {\text{x}} \right){\text{.}}{{\text{e}}^{ - x}}{\text{ - 2f '}}\left( {\text{x}} \right){\text{.}}{{\text{e}}^{ - x}}{\text{ + f}}\left( {\text{x}} \right).{e^{ - x}} \geqslant 1 \\\ {\text{f ''}}\left( {\text{x}} \right){\text{.}}{{\text{e}}^{ - x}}{\text{ - f '}}\left( {\text{x}} \right){\text{.}}{{\text{e}}^{ - x}}{\text{ - f '(x)}}{\text{.}}{{\text{e}}^{ - x}}{\text{ + f}}\left( {\text{x}} \right).{e^{ - x}} \geqslant 1 \\\ \dfrac{{d\left( {f'(x).{e^{ - x}}} \right)}}{{dx}} - \dfrac{{d\left( {f'(x).{e^{ - x}}} \right)}}{{dx}} \geqslant 1 \\\ \dfrac{{d\left( {f'(x).{e^{ - x}} - f\left( x \right).{e^{ - x}}} \right)}}{{dx}} \geqslant 1......eq\left( 1 \right) \\\ {\text{The expression }}\left( {f'(x).{e^{ - x}} - f\left( x \right).{e^{ - x}}} \right){\text{ can also be written as}} \\\ \dfrac{{d\left( {f\left( x \right).{e^{ - x}}} \right)}}{{dx}} \\\ {\text{The eq}}{\text{. 1 becomes - }} \\\ \dfrac{{{d^2}\left( {f\left( x \right).{e^{ - x}}} \right)}}{{dx}} \geqslant 1 \\\$$

Now since the double derivative of $f\left( x \right).{e^{ - x}}$ is greater than 1 it implies that it is greater than 0 as well. Hence, the function $f\left( x \right).{e^{ - x}}$is concave upwards. Let the function $f\left( x \right).{e^{ - x}}$ be g(x), for easy reference.
It is given that f(0) = f(1) = 0. This gives
g(0) = g(1) = 0.
The information collected about g(x) is-
It is concave upwards
g(0) = g(1) = 0

When we plot g(x), it should look like-

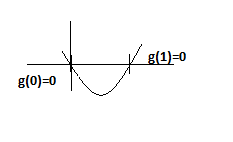
It is given to us that g(x) takes its minimum at x = ¼.
So the plot now looks like,

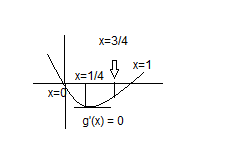
As it's given that g(x) has its minima at x= 1, so we say that g’(x) = 0.
Now,
$g'\left( x \right) = {e^{ - x}}.f'\left( x \right) - {e^{ - x}}.f\left( x \right) \\\ g'\left( x \right) = {e^{ - x}}.(f'\left( x \right) - f\left( x \right)) \\\$
For a minimum the g’(x) value changes from negative to positive.
Hence, for x values less than ¼
g’(x)<0 i.e.
$g'\left( x \right) = {e^{ - x}}.(f'\left( x \right) - f\left( x \right)) < 0$
As, e-x is an always positive term so,
$\Rightarrow (f'\left( x \right) - f\left( x \right)) < 0 \\\ \Rightarrow f'\left( x \right) < f\left( x \right) \\\$
and g’(x)>0 for x values between ¼ and 1.
$g'\left( x \right) = {e^{ - x}}.(f'\left( x \right) - f\left( x \right)) > 0 \\\ {\text{As, }}{{\text{e}}^{ - x}}{\text{ is always positive}} \\\ (f'\left( x \right) - f\left( x \right)) > 0 \\\ f'\left( x \right) > f\left( x \right){\text{ }}\forall {\text{ x}} \in {\text{(}}\dfrac{1}{4},1) \\\$

So, the correct answer is “Option C”.

Note: The point that g’(x) is negative for x< ¼ and positive for x> ¼ can be explained by the angle made by the slope. For a minima, the tan (theta) value is negative first then 0 and then positive. So this fact was used in the q.
For a maxima, the tan (theta) value first is positive then 0 and then negative.