Question

Let $\tan^{-1} y = \tan^{-1} x + \tan^{-1} \left( \frac{2x}{1-x^2} \right)$, where $|x| < \frac{1}{\sqrt{3}}$. Then a value of y is:

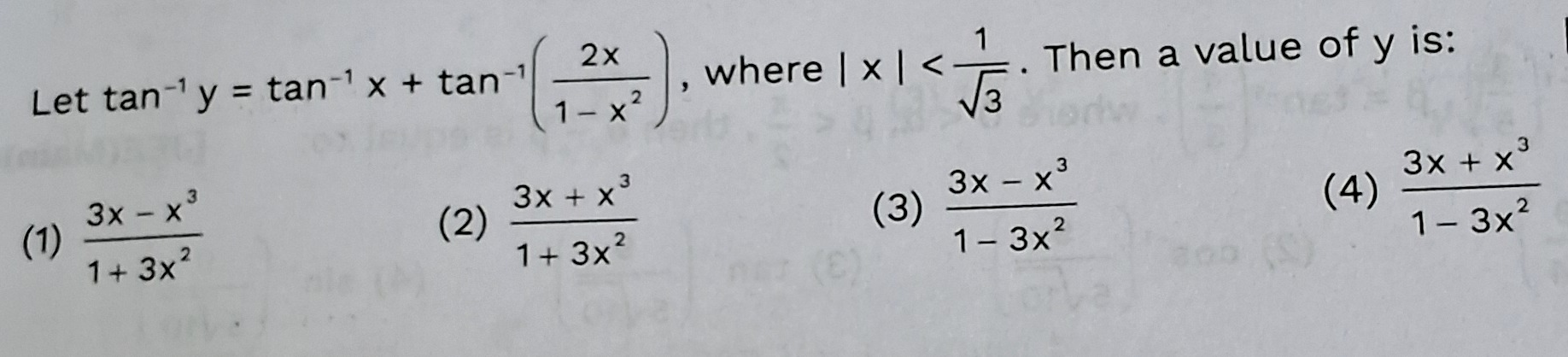
• A. $\frac{3x - x^3}{1 + 3x^2}$
• B. $\frac{3x + x^3}{1 + 3x^2}$
• C. $\frac{3x - x^3}{1 - 3x^2}$
• D. $\frac{3x + x^3}{1 - 3x^2}$

Answer 1

Answer: (C)

$\frac{3x - x^3}{1 - 3x^2}$

Answer 2

Let $x = \tan \theta$. Since $|x| < \frac{1}{\sqrt{3}}$, we have $-\frac{1}{\sqrt{3}} < x < \frac{1}{\sqrt{3}}$. This implies $-\frac{\pi}{6} < \theta < \frac{\pi}{6}$.

Now consider the term $\tan^{-1} \left( \frac{2x}{1-x^2} \right)$. Substitute $x = \tan \theta$:

$\tan^{-1} \left( \frac{2 \tan \theta}{1 - \tan^2 \theta} \right) = \tan^{-1}(\tan(2\theta)) = 2\theta$.

Substitute this back into the original equation:

$\tan^{-1} y = \tan^{-1} x + 2\theta$.

Since $x = \tan \theta$, $\tan^{-1} x = \theta$.

$\tan^{-1} y = \theta + 2\theta = 3\theta$.

We need to find $y$. Taking the tangent of both sides gives $y = \tan(3\theta)$. We use the triple angle formula for tangent:

$\tan(3\theta) = \frac{3 \tan \theta - \tan^3 \theta}{1 - 3 \tan^2 \theta}$.

Substitute $\tan \theta = x$ into this formula:

$y = \frac{3x - x^3}{1 - 3x^2}$.