Solveeit Logo
Login

Question

Question: Let $\tan^{-1} y = \tan^{-1} x + \tan^{-1} (\frac{2x}{1-x^2})$, where $|x| < \frac{1}{\sqrt{3}}$. Th...

Let tan⁡−1y=tan⁡−1x+tan⁡−1(2x1−x2)\tan^{-1} y = \tan^{-1} x + \tan^{-1} (\frac{2x}{1-x^2}), where ∣x∣<13|x| < \frac{1}{\sqrt{3}}. Then a value of y is:

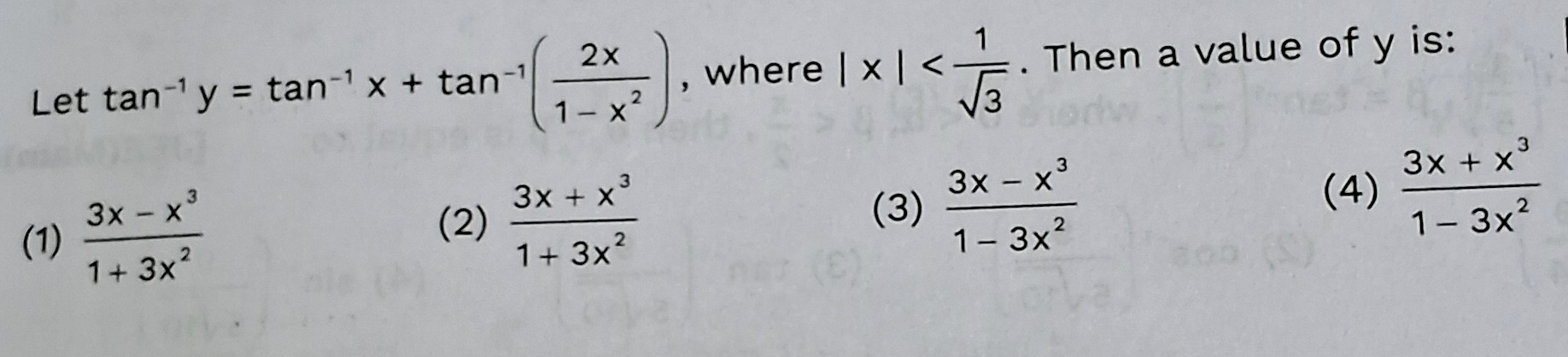
A

3x−x31+3x2\frac{3x - x^3}{1+ 3x^2}

B

3x+x31+3x2\frac{3x + x^3}{1+ 3x^2}

C

3x−x31−3x2\frac{3x - x^3}{1- 3x^2}

D

3x+x31−3x2\frac{3x + x^3}{1- 3x^2}

Answer

3x−x31−3x2\frac{3x - x^3}{1- 3x^2}

Explanation

Solution

We are given the equation tan⁡−1y=tan⁡−1x+tan⁡−1(2x1−x2)\tan^{-1} y = \tan^{-1} x + \tan^{-1} (\frac{2x}{1-x^2}) and the condition ∣x∣<13|x| < \frac{1}{\sqrt{3}}.

We can simplify the equation using the identity 2tan⁡−1x=tan⁡−1(2x1−x2)2 \tan^{-1} x = \tan^{-1} (\frac{2x}{1-x^2}), which is valid for ∣x∣<1|x| < 1. Since ∣x∣<13|x| < \frac{1}{\sqrt{3}} implies ∣x∣<1|x| < 1, we can substitute:

tan⁡−1y=tan⁡−1x+2tan⁡−1x\tan^{-1} y = \tan^{-1} x + 2 \tan^{-1} x tan⁡−1y=3tan⁡−1x\tan^{-1} y = 3 \tan^{-1} x

Now, we use the identity 3tan⁡−1x=tan⁡−1(3x−x31−3x2)3 \tan^{-1} x = \tan^{-1} (\frac{3x - x^3}{1 - 3x^2}), which is valid for ∣x∣<13|x| < \frac{1}{\sqrt{3}}. Since the given condition satisfies this, we can substitute:

tan⁡−1y=tan⁡−1(3x−x31−3x2)\tan^{-1} y = \tan^{-1} (\frac{3x - x^3}{1 - 3x^2})

Therefore, y=3x−x31−3x2y = \frac{3x - x^3}{1 - 3x^2}.