Question

Let $T_1$ & $T_2$ be two distinct common tangents to the ellipse $E: 3x^2 + 8y^2 = 48$ and the parabola $P: y^2 = 4x$. Suppose that the tangent $T_1$ touches $P$ and $E$ at the points $A_1$ & $A_2$ respectively and the tangent $T_2$ touches $P$ and $E$ at the points $A_3$ and $A_4$ respectively. Then which of the following statements is(are) true?

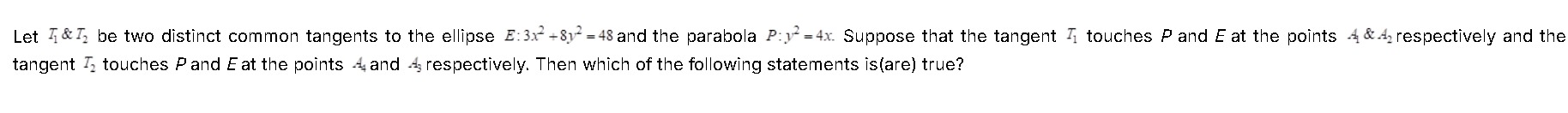
• A. The two common tangents are $y=\frac{x}{2\sqrt2}+2\sqrt2$ and $y=-\frac{x}{2\sqrt2}-2\sqrt2$
• B. The points of contact on the parabola are $A_1=(8,4\sqrt2)$ and $A_3=(8,-4\sqrt2)$
• C. The points of contact on the ellipse are $A_2=(-2,3\sqrt2/2)$ and $A_4=(-2,-3\sqrt2/2)$
• D. The tangents intersect at $(-8,0)$

Answer 1

Answer: (A), (B), (C), (D)

All of the above statements are true.

Answer 2

Here's a breakdown of the solution:

1. Find the common tangents:

   • Express the tangent to the parabola $P: y^2 = 4x$ in slope-intercept form: $y = mx + \frac{1}{m}$.
   • Express the ellipse as $\frac{x^2}{16} + \frac{y^2}{6} = 1$.
   • Use the tangency condition for the ellipse: $c^2 = 16m^2 + 6$, where $y = mx + c$ is tangent.
   • Equate $c = \frac{1}{m}$ and solve for $m$. You should find $m = \pm \frac{1}{2\sqrt{2}}$.
   • The two tangents are therefore $T_1: y = \frac{x}{2\sqrt{2}} + 2\sqrt{2}$ and $T_2: y = -\frac{x}{2\sqrt{2}} - 2\sqrt{2}$.

2. Find the points of contact on the parabola:

   • Use the formula for the point of tangency on $y^2 = 4x$: $(\frac{1}{m^2}, \frac{2}{m})$.
   • For $T_1$, $m = \frac{1}{2\sqrt{2}}$, so $A_1 = (8, 4\sqrt{2})$.
   • For $T_2$, $m = -\frac{1}{2\sqrt{2}}$, so $A_3 = (8, -4\sqrt{2})$.

3. Find the points of contact on the ellipse:

   • Substitute the tangent equations into the ellipse equation $3x^2 + 8y^2 = 48$.
   • For $T_1$, you should find $x = -2$. Then $y = \frac{-2}{2\sqrt{2}} + 2\sqrt{2} = \frac{3\sqrt{2}}{2}$, so $A_2 = (-2, \frac{3\sqrt{2}}{2})$.
   • For $T_2$, you should find $x = -2$. Then $y = -\frac{-2}{2\sqrt{2}} - 2\sqrt{2} = -\frac{3\sqrt{2}}{2}$, so $A_4 = (-2, -\frac{3\sqrt{2}}{2})$.

4. Find the intersection of the tangents:

   • Solve the system of equations: $y = \frac{x}{2\sqrt{2}} + 2\sqrt{2}$ $y = -\frac{x}{2\sqrt{2}} - 2\sqrt{2}$
   • Adding the equations gives $\frac{x}{\sqrt{2}} = -4\sqrt{2}$, so $x = -8$. Thus $y = 0$, and the intersection point is $(-8, 0)$.

Therefore, all given statements are true.