Question
Question: Let $\sum_{k=1}^{\infty} \frac{1}{k^2} = \frac{\pi^2}{6}$ and $S_i = \sum_{k=1}^{\infty} \frac{i}{(3...
Let ∑k=1∞k21=6π2 and Si=∑k=1∞(36k2−1)ii, then
S1+S2=
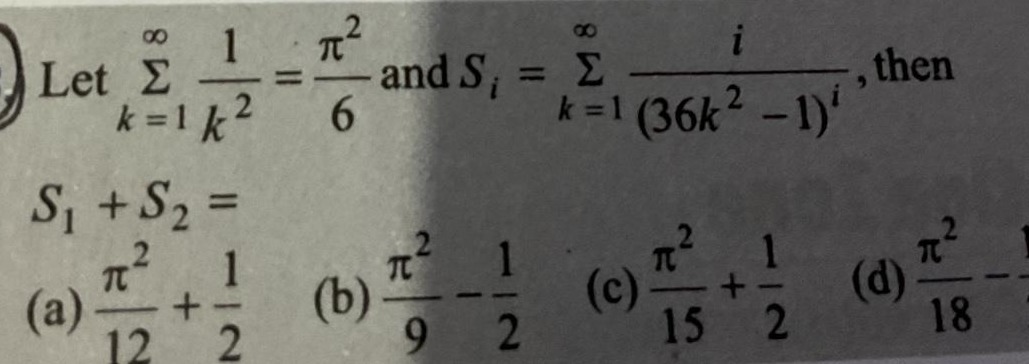
12π2+21
9π2−21
15π2+21
18π2−21
18π2−21
Solution
Solution Explanation:
-
Write
S₁ = ∑ₖ₌₁∞ 1/(36k² – 1) = ∑ₖ₌₁∞ 1/[(6k–1)(6k+1)].
Using partial fractions,
1/(6k–1)(6k+1) = ½[1/(6k–1) – 1/(6k+1)]. -
Express S₁ in a form involving ∑ₖ₌₁∞ 1/(k² – 1/36) by noting
36k² – 1 = 36[k² – (1/6)²].
Thus, S₁ = 1/36 ∑ₖ₌₁∞ 1/(k² – (1/6)²). -
Use the known formula (valid for a non‐integer a):
∑ₖ₌₁∞ 1/(k² – a²) = 1/(2a²) – (π/(2a))cot(πa).
For a = 1/6, one obtains
S₁ = 1/36 [ 18 – 3π cot(π/6) ] = (6 – π√3)/12
(since cot(π/6)=√3). -
Similarly, express
S₂ = ∑ₖ₌₁∞ 2/(36k² – 1)² = 2/36² ∑ₖ₌₁∞ 1/(k² – (1/6)²)². -
Use the formula
∑ₖ₌₁∞ 1/(k² – a²)² = [π/(4a³)]cot(πa) + [π²/(4a²)]csc²(πa) – 1/(2a⁴).
For a = 1/6, compute the terms noting:
(1/6)³ = 1/216, (1/6)⁴ = 1/1296, cot(π/6)=√3, csc(π/6)=2, csc²(π/6)=4.
This yields
∑ₖ₌₁∞ 1/(k² – (1/6)²)² = 54π√3 + 36π² – 648.
Thus,
S₂ = 2/(1296) (54π√3 + 36π² – 648) = (6π√3 + 4π² – 72)/72. -
Combine S₁ and S₂ with common denominator (convert S₁ to denominator 72):
S₁ = (6 – π√3)/12 = (36 – 6π√3)/72.
Then,
S₁ + S₂ = [ (36 – 6π√3) + (6π√3 + 4π² – 72) ]/72
= (4π² – 36)/72 = (π² – 9)/18.
This can be written as
π²/18 – 1/2.
Answer:
Option (d): 18π2−21
