Question

Let $\sqrt{3}\hat{i}+j$, $\hat{i}+\sqrt{3}\hat{j}$ and $\beta \hat{i}+\left( 1-\beta \right)\hat{j}$ respectively be the position vectors of the points A, B and c with respect to the origin O. if the distance of C from the bisector of the acute angle between OA and OB is $\dfrac{3}{\sqrt{2}}$, then the sum of all possible values of $\beta$ is
(a) 2
(b) 1
(c) 3
(d) 4

Answer 1

We can solve this question with two method, i.e. vector method or 2D coordinate method. We will choose the latter method as it is easier. We will convert the position vectors of the points into coordinates. Then, we will find the inclination of OA and OB with respect to the x-axis. We know that the inclination of any line with respect to the x-axis is given by $\theta ={{\tan }^{-1}}\left( m \right)$, where m is the slope of the line. Once we get these angles, we will find the inclination of the angle bisector and find the slope as $m=\tan \theta$. Now, we can find the line equation of the angle bisector in the slope point form as we know that origin lies on the line. Once we get the line equation, we know that distance of any point from a line $ax+by+c=0$ is given as $d=\dfrac{\left| a\left( {{x}_{1}} \right)+b\left( {{y}_{1}} \right)+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$, where $\left( {{x}_{1}},{{y}_{1}} \right)$ is the coordinates of the point from which distance is to be found. We will substitute point C and find all the possible values of $\beta$. Then we will add all those values to find the answer.

Complete step-by-step solution:
The point A, B and C given to us are $\sqrt{3}\hat{i}+j$, $\hat{i}+\sqrt{3}\hat{j}$ and $\beta \hat{i}+\left( 1-\beta \right)\hat{j}$ respectively. We know that the coefficient of $\hat{i}$ is the x – coordinate of the point and coefficient of $\hat{j}$ is the y – coordinate of the point.
Therefore, points A, B and C are $\left( \sqrt{3},1 \right)$, $\left( 1,\sqrt{3} \right)$ and $\left( \beta ,1-\beta \right)$ respectively.

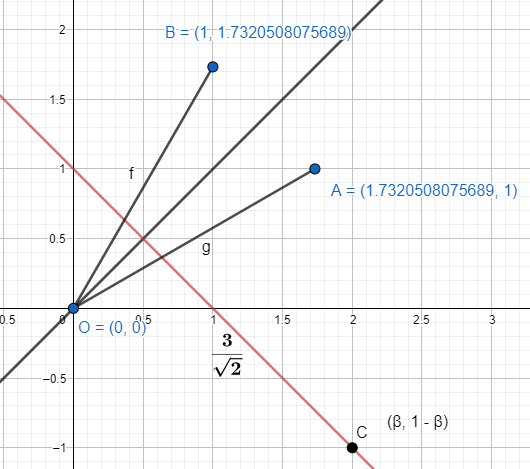
Now, the slope of line formed by any two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given as $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$.
$\Rightarrow$ Slope of line OA is ${{m}_{OA}}=\dfrac{1}{\sqrt{3}}$.
$\Rightarrow$ Slope of line OB is ${{m}_{OB}}=\dfrac{\sqrt{3}}{1}$.
Now, we know that inclination of any line with the x-axis is given as $\theta ={{\tan }^{-1}}\left( m \right)$, where m is the slope of the line.
$\Rightarrow$ Inclination of line OA is ${{\theta }_{OA}}={{\tan }^{-1}}\left( \dfrac{1}{\sqrt{3}} \right)=\dfrac{\pi }{6}$.
$\Rightarrow$ Inclination of line OB is ${{\theta }_{OB}}={{\tan }^{-1}}\left( \sqrt{3} \right)=\dfrac{\pi }{3}$.
Therefore, the inclination of the angle bisector of OA and OB will be $\dfrac{1}{2}\left( \dfrac{\pi }{6}+\dfrac{\pi }{3} \right)=\dfrac{\pi }{4}$.
We know that the slope of any line is $m=\tan \theta$.
$\Rightarrow$ Slope of angle bisector $m=\tan \left( \dfrac{\pi }{4} \right)=1$.
The angle bisector passes through the intersection of OA and OB that is O.
Therefore, equation of angle bisector in slope point form is given as follows:
$\begin{aligned} & \Rightarrow \left( y-0 \right)=\left( 1 \right)\left( x-0 \right) \\\ & \Rightarrow x-y=0 \\\ \end{aligned}$
We also know that distance of any point from a line $ax+by+c=0$ is given as $d=\dfrac{\left| a\left( {{x}_{1}} \right)+b\left( {{y}_{1}} \right)+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$, where $\left( {{x}_{1}},{{y}_{1}} \right)$ is the coordinates of the point from which distance is to be found. We will substitute point C. The distance is given to us as $\dfrac{3}{\sqrt{2}}$.
$\begin{aligned} & \Rightarrow \dfrac{3}{\sqrt{2}}=\dfrac{\left| 1\left( \beta \right)-1\left( 1-\beta \right) \right|}{\sqrt{{{1}^{2}}+{{1}^{2}}}} \\\ & \Rightarrow \left| 2\beta -1 \right|=3 \\\ & \Rightarrow 2\beta -1=\pm 3 \\\ \end{aligned}$
Therefore, $\beta =2$ or $\beta =-1$
Thus, sum of all the values of $\beta$ is 2 – 1 = 1.
Hence, option (b) is the correct option.

Note: We are able to convert the position vectors in coordinates because we are dealing only with $\hat{i}$ and $\hat{j}$ components. If there was a $\hat{k}$ component, we will have a z – coordinate, which will make the problem more complex.