Solveeit Logo
Login

Question

Physics Question on Electric Field

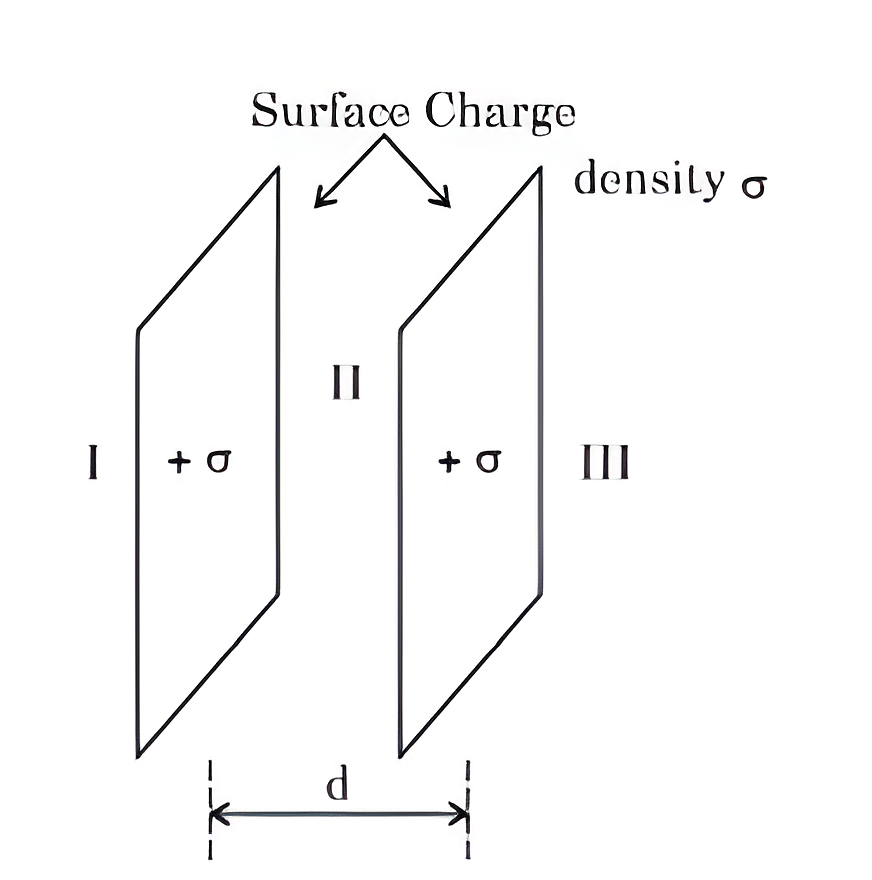
Let σ\sigma be the uniform surface charge density of two infinite thin plane sheets shown in figure Then the electric fields in three different region EI,EIIE_I, E_{I I} and EIIIE_{I I I} are:

A

E⃗I=0,E⃗II=σϵ0n^,EIII=0\vec{E}_I=0, \vec{E}_{I I}=\frac{\sigma}{\epsilon_0} \hat{n}, E_{I I I}=0

B

E⃗I=2σϵ0n^,E⃗II=0,E⃗III=2σϵ0n^\vec{E}_I=\frac{2 \sigma}{\epsilon_0} \hat{n}, \vec{E}_{I I}=0, \vec{E}_{I I I}=\frac{2 \sigma}{\epsilon_0} \hat{n}

C

E⃗I=−σϵ0n^,E⃗II=0,E⃗III=σϵ0n^\vec{E}_I=-\frac{\sigma}{\epsilon_0} \hat{n}, \vec{E}_{I I}=0, \vec{E}_{I I I}=\frac{\sigma}{\epsilon_0} \hat{n}

D

E⃗I=σ2ϵ0n^,E⃗II=0,E⃗III=σ2ϵ0n^\vec{E}_I=\frac{\sigma}{2 \epsilon_0} \hat{n}, \vec{E}_{I I}=0, \vec{E}_{I I I}=\frac{\sigma}{2 \epsilon_0} \hat{n}

Answer

E⃗I=−σϵ0n^,E⃗II=0,E⃗III=σϵ0n^\vec{E}_I=-\frac{\sigma}{\epsilon_0} \hat{n}, \vec{E}_{I I}=0, \vec{E}_{I I I}=\frac{\sigma}{\epsilon_0} \hat{n}

Explanation

Solution

The correct answer is (C) : E⃗I=−σϵ0n^,E⃗II=0,E⃗III=σϵ0n^\vec{E}_I=-\frac{\sigma}{\epsilon_0} \hat{n}, \vec{E}_{I I}=0, \vec{E}_{I I I}=\frac{\sigma}{\epsilon_0} \hat{n}
Assuming RHS to be n^
EI​=2ϵ0​σ​(−n^)+2ϵ0​σ​(−n^)=−ϵ0​σ​n^
EII​=0
EIII​=2ϵ0​σ​(n^)+2ϵ0​σ​(n^)=ϵ0​σ​(n^)