Question
Question: Let $S_n = \sum_{k=1}^{n} \frac{n}{n^2 + kn + k^2}$ and $T_n = \sum_{k=0}^{n-1} \frac{n}{n^2 + kn + ...
Let Sn=∑k=1nn2+kn+k2n and Tn=∑k=0n−1n2+kn+k2n for n = 1, 2, 3, ...... Then
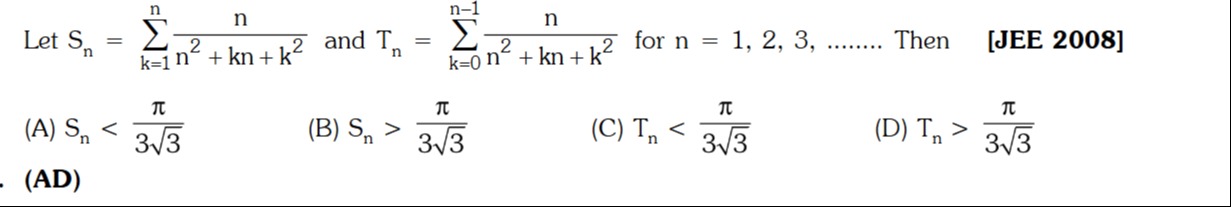
S_n < \frac{\pi}{3\sqrt{3}}
S_n > \frac{\pi}{3\sqrt{3}}
T_n < \frac{\pi}{3\sqrt{3}}
T_n > \frac{\pi}{3\sqrt{3}}
A, D
Solution
The sums Sn and Tn can be rewritten as Riemann sums for the integral ∫011+x+x21dx. Sn=∑k=1n1+(k/n)+(k/n)21/n is a right Riemann sum. Tn=∑k=0n−11+(k/n)+(k/n)21/n is a left Riemann sum. The function f(x)=1+x+x21 is strictly decreasing on [0,1] because its derivative f′(x)=−(1+x+x2)21+2x is negative for x∈[0,1]. The integral evaluates to ∫011+x+x21dx=33π. For a strictly decreasing function, the right Riemann sum is always less than the integral, and the left Riemann sum is always greater than the integral. Therefore, Sn<∫01f(x)dx and Tn>∫01f(x)dx. This implies Sn<33π and Tn>33π.
