Question

Let S = {$\sqrt{n}$ : 1 < n < 50 and n is odd}

Let a ∈ S and A= $\begin{bmatrix} 1 & 0 & a \\ -1 & 1 & 0 \\ -a & 0 & 1 \end{bmatrix}$

If $\sum_{a \in S}$det($adjA$) = 100$\lambda$, then $\lambda$, is equal to

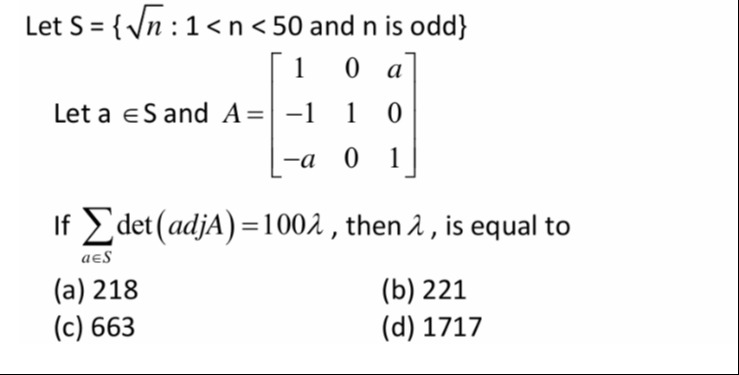
• A. 218
• B. 221
• C. 663
• D. 1717

Answer 1

Answer: (B)

221

Answer 2

The set S contains elements of the form $\sqrt{n}$ where n is an odd integer such that 1 < n < 50.

The odd integers n satisfying 1 < n < 50 are 3, 5, 7, ..., 49.

So, S = {$\sqrt{3}, \sqrt{5}, \sqrt{7}, ..., \sqrt{49}$}.

Let $a \in S$. The matrix A is given by $A = \begin{bmatrix} 1 & 0 & a \\ -1 & 1 & 0 \\ -a & 0 & 1 \end{bmatrix}$

We need to calculate det(adjA). For a square matrix A of order n, det(adjA) = (detA)$^{n-1}$. Here n=3, so det(adjA) = (detA)$^2$.

First, calculate the determinant of A: det(A) = $1 \begin{vmatrix} 1 & 0 \\ 0 & 1 \end{vmatrix} - 0 \begin{vmatrix} -1 & 0 \\ -a & 1 \end{vmatrix} + a \begin{vmatrix} -1 & 1 \\ -a & 0 \end{vmatrix}$

det(A) = $1(1 \times 1 - 0 \times 0) - 0 + a((-1) \times 0 - 1 \times (-a))$

det(A) = $1(1) + a(0 + a) = 1 + a^2$.

Since $a \in S$, $a = \sqrt{n}$ for some odd integer n with 1 < n < 50. Thus, $a^2 = n$, and $n \ge 3$. So det(A) = $1+n \ge 4$, which means A is invertible and the formula det(adjA) = (detA)$^2$ is valid.

det(adjA) = $(1+a^2)^2$.

The given condition is $\sum_{a \in S}$det(adjA) = 100$\lambda$.

Substituting det(adjA) and the form of a: $\sum_{a \in S} (1+a^2)^2 = 100\lambda$.

Since $a \in S$, $a = \sqrt{n}$ where n is an odd integer from 3 to 49. Thus $a^2 = n$.

The sum becomes $\sum_{n \in \{3, 5, ..., 49\}, n \text{ is odd}} (1+n)^2$.

The values of n are 3, 5, 7, ..., 49.

The values of $1+n$ are $1+3=4, 1+5=6, 1+7=8, ..., 1+49=50$.

The sum is $4^2 + 6^2 + 8^2 + ... + 50^2$.

This is a sum of squares of even numbers. We can write each term as $(2k)^2$.

$4 = 2 \times 2$, so $4^2 = (2 \times 2)^2$.

$6 = 2 \times 3$, so $6^2 = (2 \times 3)^2$.

$8 = 2 \times 4$, so $8^2 = (2 \times 4)^2$.

...

$50 = 2 \times 25$, so $50^2 = (2 \times 25)^2$.

The sum is $\sum_{k=2}^{25} (2k)^2$.

$\sum_{k=2}^{25} (2k)^2 = \sum_{k=2}^{25} 4k^2 = 4 \sum_{k=2}^{25} k^2$.

We use the formula for the sum of the first m squares: $\sum_{k=1}^{m} k^2 = \frac{m(m+1)(2m+1)}{6}$.

$\sum_{k=2}^{25} k^2 = \sum_{k=1}^{25} k^2 - 1^2$.

$\sum_{k=1}^{25} k^2 = \frac{25(25+1)(2 \times 25 + 1)}{6} = \frac{25 \times 26 \times 51}{6}$.

$\frac{25 \times 26 \times 51}{6} = \frac{25 \times (2 \times 13) \times (3 \times 17)}{2 \times 3} = 25 \times 13 \times 17$.

$25 \times 13 = 325$.

$325 \times 17 = 325 \times (10+7) = 3250 + 325 \times 7 = 3250 + 2275 = 5525$.

So, $\sum_{k=1}^{25} k^2 = 5525$.

Now, $\sum_{k=2}^{25} k^2 = \sum_{k=1}^{25} k^2 - 1^2 = 5525 - 1 = 5524$.

The sum $\sum_{a \in S}$det(adjA) is $4 \times \sum_{k=2}^{25} k^2 = 4 \times 5524$.

$4 \times 5524 = 22096$.

The given equation is $\sum_{a \in S}$det(adjA) = 100$\lambda$.

$22096 = 100\lambda$.

$\lambda = \frac{22096}{100} = 220.96$.

The calculated value of $\lambda$ is 220.96, which is not among the given options (218, 221, 663, 1717). This discrepancy suggests a potential error in the problem statement or the provided options. However, based on the standard properties of matrices and determinants, and careful calculation, the steps followed are correct.

Given the options, the most plausible answer is 221. This suggests that the value on the left side of the equation should have been 22100 instead of 22096. This could happen if, for example, the sum was meant to include one more term or exclude one term, or if the coefficient was slightly different.