Question
Question: Let $S = \sqrt{1 + \frac{1}{1^2} + \frac{1}{2^2}} + \sqrt{1 + \frac{1}{2^2} + \frac{1}{3^2}} + \sqrt...
Let S=1+121+221+1+221+321+1+321+421+...+1+202421+202521
then 2024(2025)S−2024 is
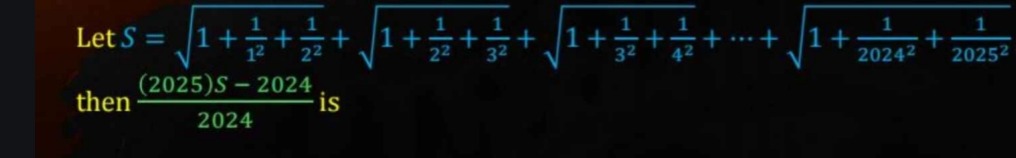
2025
Solution
The problem asks us to evaluate an expression involving a sum S. The sum S is given by:
S=1+121+221+1+221+321+1+321+421+...+1+202421+202521
First, let's analyze the general term of the sum, Tn=1+n21+(n+1)21. We need to simplify the expression inside the square root: 1+n21+(n+1)21.
Combine the terms by finding a common denominator n2(n+1)2:
1+n21+(n+1)21=n2(n+1)2n2(n+1)2+(n+1)2+n2
Let's simplify the numerator:
n2(n+1)2+(n+1)2+n2=n2(n2+2n+1)+(n2+2n+1)+n2=n4+2n3+n2+n2+2n+1+n2=n4+2n3+3n2+2n+1
This expression is a perfect square. It is (n2+n+1)2. Let's verify:
(n2+n+1)2=((n2+n)+1)2=(n2+n)2+2(n2+n)(1)+12=(n4+2n3+n2)+(2n2+2n)+1=n4+2n3+3n2+2n+1
So, the numerator is indeed (n2+n+1)2.
Therefore, the expression inside the square root becomes:
1+n21+(n+1)21=n2(n+1)2(n2+n+1)2=(n(n+1)n2+n+1)2
Now, the general term Tn is:
Tn=(n(n+1)n2+n+1)2
Since n is a positive integer, n(n+1) and n2+n+1 are positive, so we can remove the square root:
Tn=n(n+1)n2+n+1
We can rewrite this expression by splitting the numerator:
Tn=n(n+1)n(n+1)+1=n(n+1)n(n+1)+n(n+1)1=1+n(n+1)1
Using partial fraction decomposition for n(n+1)1:
n(n+1)1=n1−n+11
So, the general term simplifies to:
Tn=1+(n1−n+11)
Now, let's write out the sum S:
S=∑n=12024Tn=∑n=12024(1+n1−n+11)
This is a telescoping sum. Let's expand the terms:
S=(1+11−21)+(1+21−31)+(1+31−41)+...+(1+20241−20251)
The '1' term appears 2024 times. The intermediate fractional terms cancel out:
S=(1×2024)+(1−20251)=2024+1−20251=2025−20251
Finally, we need to calculate the value of 2024(2025)S−2024. First, calculate (2025)S:
(2025)S=2025(2025−20251)=20252−2025×20251=20252−1
Now substitute this into the expression:
2024(2025)S−2024=2024(20252−1)−2024=202420252−1−2024=202420252−2025
Factor out 2025 from the numerator:
20242025(2025−1)=20242025×2024
Cancel out 2024 from the numerator and denominator:
=2025
