Question

Let S\left( \alpha \right)=\left\\{ \left( x,y \right):{{y}^{2}}\le x,0\le x\le \alpha \right\\} and $A\left( \alpha \right)$is area of the region $S\left( \alpha \right)$. If for a $\lambda ,0<\lambda <4,A\left( \lambda \right):A\left( 4 \right)=2:5,$ then $\lambda$ equals
A. $2{{\left( \dfrac{4}{25} \right)}^{\dfrac{1}{3}}}$
B. $4{{\left( \dfrac{2}{5} \right)}^{\dfrac{1}{3}}}$
C. $4{{\left( \dfrac{4}{25} \right)}^{\dfrac{1}{3}}}$
D. $2{{\left( \dfrac{2}{5} \right)}^{\dfrac{1}{3}}}$

Answer 1

First we will plot the graph and identify the region for $A\left( \lambda \right)$ then we will write the given parabolic equation in form of x and integrate it from $x=0\text{ to }x=\lambda$, after integrating we will simply apply the final condition given in the question and then obtain the value of $\lambda$.

Complete step by step answer:
Given that, S\left( \alpha \right)=\left\\{ \left( x,y \right):{{y}^{2}}\le x,0\le x\le \alpha \right\\} and $A\left( \alpha \right)$is area of the region $S\left( \alpha \right)$:

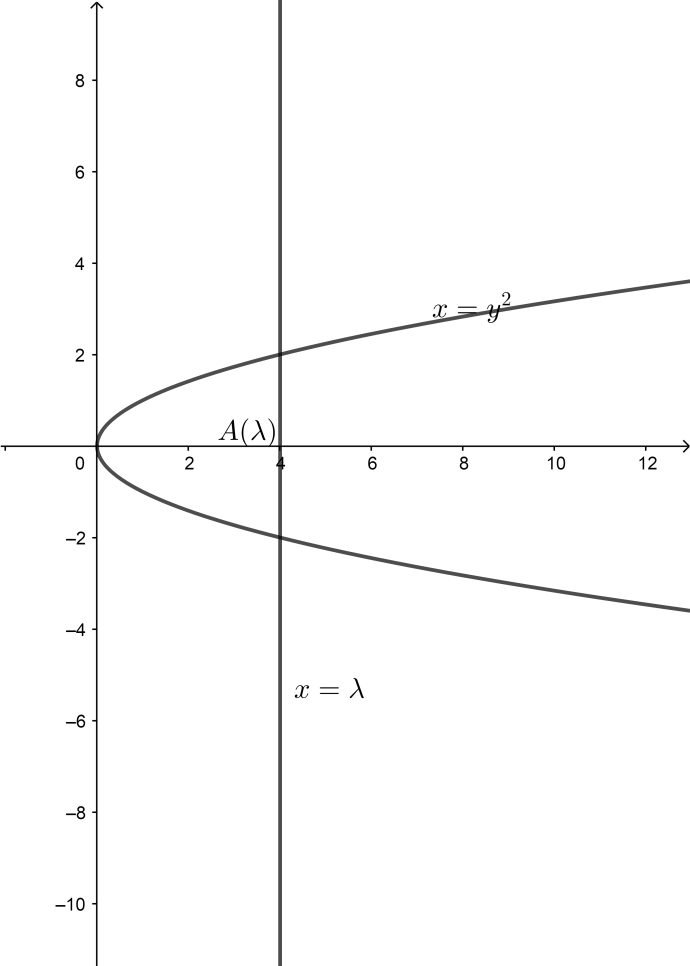
Now, We see that $A\left( \lambda \right)$ is the region bounded by $x={{y}^{2}}$ from $x=0\text{ to }x=\lambda$, so to find $A\left( \lambda \right)$ we will integrate the parabolic equation from $0$ to $\lambda$ :
To start the integration first write the equation in form of x such that: $x={{y}^{2}}\Rightarrow y=\sqrt{x}$
Now we will integrate the following, to integrate it we will use the power rule that is : $\int{f{{(x)}^{n}}dx=\dfrac{f{{(x)}^{n+1}}}{n+1}}$
So:
$\begin{aligned} & A\left( \lambda \right)=2\int\limits_{0}^{\lambda }{\sqrt{x}}dx\Rightarrow 2{{\left[ \dfrac{\left( {{x}^{\dfrac{1}{2}+1}} \right)}{\left( \dfrac{1}{2}+1 \right)} \right]}^{\lambda }}_{0} \\\ & \Rightarrow 2{{\left[ \dfrac{\left( {{x}^{\dfrac{3}{2}}} \right)}{\left( \dfrac{3}{2} \right)} \right]}^{\lambda }}_{0} \\\ \end{aligned}$
Now we will apply the upper limit and the lower limit into the obtained integral we get:
$2{{\left[ \dfrac{\left( {{x}^{\dfrac{3}{2}}} \right)}{\left( \dfrac{3}{2} \right)} \right]}^{\lambda }}_{0}\Rightarrow 2\left[ \dfrac{\left( {{\lambda }^{\dfrac{3}{2}}} \right)}{\left( \dfrac{3}{2} \right)} \right]-2\left[ \dfrac{\left( {{0}^{\dfrac{3}{2}}} \right)}{\left( \dfrac{3}{2} \right)} \right]\Rightarrow \dfrac{4}{3}{{\lambda }^{\dfrac{3}{2}}}$
Therefore , $A\left( \lambda \right)=\dfrac{4}{3}{{\lambda }^{\dfrac{3}{2}}}\text{ }.......\text{Equation 1}\text{.}$
Now it is given in the question that: $\dfrac{A(\lambda )}{A(4)}=\dfrac{2}{5},(0<\lambda <4)$
We will put the value of $A\left( \lambda \right)$ from equation 1 into the above mentioned equation:

& \dfrac{A(\lambda )}{A(4)}=\dfrac{2}{5} \\\ & \Rightarrow \dfrac{\left( \dfrac{4}{3}{{\lambda }^{\dfrac{3}{2}}} \right)}{\left( \dfrac{4}{3}{{4}^{\dfrac{3}{2}}} \right)}=\dfrac{2}{5}\Rightarrow \dfrac{{{\lambda }^{\dfrac{3}{2}}}}{{{4}^{\dfrac{3}{2}}}}=\dfrac{2}{5} \\\ \end{aligned}$$ Now we will square both the sides: $$\begin{aligned} & \Rightarrow {{\left( \dfrac{{{\lambda }^{\dfrac{3}{2}}}}{{{4}^{\dfrac{3}{2}}}} \right)}^{2}}={{\left( \dfrac{2}{5} \right)}^{2}} \\\ & \Rightarrow {{\left( \dfrac{\lambda }{4} \right)}^{3}}={{\left( \dfrac{2}{5} \right)}^{2}}\Rightarrow {{\left( \dfrac{\lambda }{4} \right)}^{3}}=\left( \dfrac{4}{25} \right) \\\ \end{aligned}$$ Again we will be taking cube roots on both sides: $$\Rightarrow \left( \dfrac{\lambda }{4} \right)={{\left( \dfrac{4}{25} \right)}^{\dfrac{1}{3}}}\Rightarrow \lambda =4{{\left( \dfrac{4}{25} \right)}^{\dfrac{1}{3}}}$$ Therefore the correct answer is option C.** **Note:** Remember that a region bounded from point $a$ to $b$ means that integration will be done from the lower limit $a$ and the upper limit $b$ . Also take care when you take the cube roots while finding the final value of $\lambda $, we have written the cube roots as raising the fraction or number to the power of $\dfrac{1}{3}$ . Students can make the mistake while solving the terms raised with power so one must learn the properties of powers.