Question

Let S denotes the set of all points where $\sqrt[5]{x^2 |x^3|} - \sqrt[3]{x^2 |x|-1}$ is not differentiable then S is a subset of:

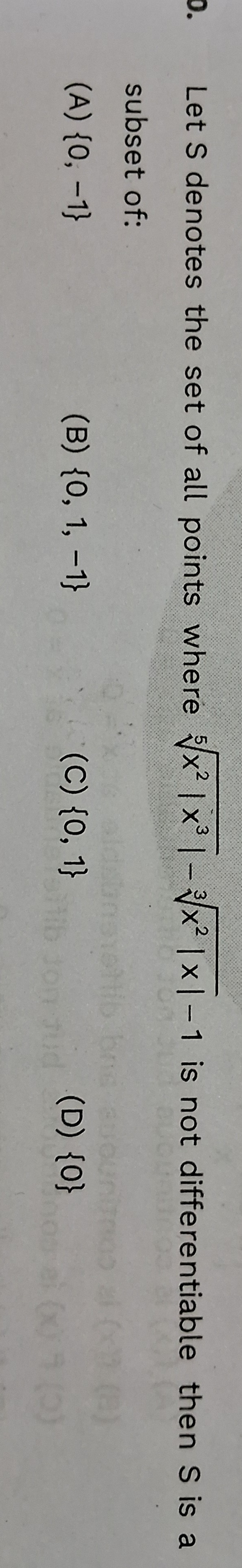
• A. {0, -1}
• B. {0, 1, -1}
• C. {0, 1}
• D. {0}

Answer 1

Answer: (B)

{0, 1, -1}

Answer 2

The given function is $f(x) = \sqrt[5]{x^2 |x^3|} - \sqrt[3]{x^2 |x|-1}$. Let's analyze each term separately for differentiability.

First term: $g(x) = \sqrt[5]{x^2 |x^3|}$

We know that $|x^3| = |x|^3$. So, $g(x) = \sqrt[5]{x^2 |x|^3}$.

Case 1: $x \ge 0$

For $x \ge 0$, $|x| = x$. $g(x) = \sqrt[5]{x^2 \cdot x^3} = \sqrt[5]{x^5} = x$. The derivative $g'(x) = 1$ for $x > 0$.

Case 2: $x < 0$

For $x < 0$, $|x| = -x$. $g(x) = \sqrt[5]{x^2 (-x)^3} = \sqrt[5]{x^2 (-x^3)} = \sqrt[5]{-x^5}$. Since the fifth root is an odd root, $\sqrt[5]{-A} = -\sqrt[5]{A}$. So, $g(x) = -\sqrt[5]{x^5} = -x$. The derivative $g'(x) = -1$ for $x < 0$.

Combining these, $g(x) = \begin{cases} x & x \ge 0 \\ -x & x < 0 \end{cases}$, which is the definition of $g(x) = |x|$.

The function $g(x) = |x|$ is continuous everywhere but is not differentiable at $x=0$. The left-hand derivative at $x=0$ is $-1$, and the right-hand derivative at $x=0$ is $1$. Since they are not equal, $g(x)$ is not differentiable at $x=0$.

Second term: $h(x) = \sqrt[3]{x^2 |x|-1}$

Let $u(x) = x^2 |x|-1$. Then $h(x) = (u(x))^{1/3}$.

Let's analyze $u(x)$:

Case 1: $x \ge 0$

$u(x) = x^2 \cdot x - 1 = x^3 - 1$. The derivative $u'(x) = 3x^2$ for $x > 0$.

Case 2: $x < 0$

$u(x) = x^2 (-x) - 1 = -x^3 - 1$. The derivative $u'(x) = -3x^2$ for $x < 0$.

Let's check differentiability of $u(x)$ at $x=0$:

$u(0) = 0^2|0|-1 = -1$.

Left Hand Derivative (LHD) at $x=0$: $\lim_{h \to 0^-} \frac{u(0+h) - u(0)}{h} = \lim_{h \to 0^-} \frac{(-h^3 - 1) - (-1)}{h} = \lim_{h \to 0^-} \frac{-h^3}{h} = \lim_{h \to 0^-} (-h^2) = 0$.

Right Hand Derivative (RHD) at $x=0$: $\lim_{h \to 0^+} \frac{u(0+h) - u(0)}{h} = \lim_{h \to 0^+} \frac{(h^3 - 1) - (-1)}{h} = \lim_{h \to 0^+} \frac{h^3}{h} = \lim_{h \to 0^+} (h^2) = 0$.

Since LHD = RHD = 0, $u(x)$ is differentiable at $x=0$ and $u'(0)=0$. Thus, $u(x)$ is differentiable for all $x \in \mathbb{R}$.

Now consider $h(x) = (u(x))^{1/3}$. The derivative is $h'(x) = \frac{1}{3} (u(x))^{-2/3} u'(x) = \frac{u'(x)}{3 (u(x))^{2/3}}$.

For $h(x)$ to be differentiable, $u(x)$ must be differentiable, and $u(x)$ must not be zero (because of the term $(u(x))^{-2/3}$ in the denominator). If $u(x)=0$ and $u'(x) \ne 0$, then $h'(x)$ will approach infinity, meaning $h(x)$ is not differentiable (it has a vertical tangent).

Let's find the values of $x$ for which $u(x)=0$:

If $x \ge 0$: $u(x) = x^3 - 1 = 0 \implies x^3 = 1 \implies x = 1$. At $x=1$, $u(1)=0$. $u'(1) = 3(1)^2 = 3$. Since $u(1)=0$ and $u'(1) \ne 0$, $h(x)$ is not differentiable at $x=1$.

If $x < 0$: $u(x) = -x^3 - 1 = 0 \implies -x^3 = 1 \implies x^3 = -1 \implies x = -1$. At $x=-1$, $u(-1)=0$. $u'(-1) = -3(-1)^2 = -3$. Since $u(-1)=0$ and $u'(-1) \ne 0$, $h(x)$ is not differentiable at $x=-1$.

Also, $h(x)$ is differentiable at $x=0$ because $u(0)=-1 \ne 0$. In fact, $h'(0) = \frac{u'(0)}{3(u(0))^{2/3}} = \frac{0}{3(-1)^{2/3}} = \frac{0}{3(1)} = 0$.

Points of non-differentiability for $f(x) = g(x) - h(x)$

The function $f(x)$ is the difference of two functions.

• If $g(x)$ is differentiable at a point and $h(x)$ is not differentiable at that point, then $f(x)$ is not differentiable at that point.
• If $g(x)$ is not differentiable at a point and $h(x)$ is differentiable at that point, then $f(x)$ is not differentiable at that point.
• If both $g(x)$ and $h(x)$ are not differentiable at a point, then $f(x)$ may or may not be differentiable. We need to check explicitly.

Let's examine the points of concern: $x=0, x=1, x=-1$.

1. At $x=0$:

   • $g(x) = |x|$ is not differentiable at $x=0$.
   • $h(x) = \sqrt[3]{x^2|x|-1}$ is differentiable at $x=0$ (as $u(0)=-1 \ne 0$).

   Since $f(x)$ is the difference of a non-differentiable function and a differentiable function at $x=0$, $f(x)$ is not differentiable at $x=0$.

2. At $x=1$:

   • $g(x) = |x|$ is differentiable at $x=1$ (since $x>0$, $g(x)=x$, so $g'(1)=1$).
   • $h(x) = \sqrt[3]{x^2|x|-1}$ is not differentiable at $x=1$.

   Since $f(x)$ is the difference of a differentiable function and a non-differentiable function at $x=1$, $f(x)$ is not differentiable at $x=1$.

3. At $x=-1$:

   • $g(x) = |x|$ is differentiable at $x=-1$ (since $x<0$, $g(x)=-x$, so $g'(-1)=-1$).
   • $h(x) = \sqrt[3]{x^2|x|-1}$ is not differentiable at $x=-1$.

   Since $f(x)$ is the difference of a differentiable function and a non-differentiable function at $x=-1$, $f(x)$ is not differentiable at $x=-1$.

Therefore, the set S of all points where $f(x)$ is not differentiable is $S = \{0, 1, -1\}$.