Question

Let $S = \begin{Bmatrix} m \in \mathbb{Z}: A^{m^2} + A^m = 3I - A^{-6} \end{Bmatrix}$, where $A = \begin{bmatrix} 2 & -1 \\ 1 & 0 \end{bmatrix}$. Then n(S) is equal to ______.

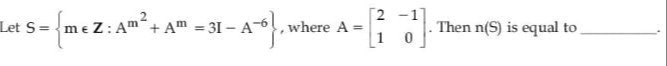
Answer 1

2

Answer 2

Solution:

Given

$$A=\begin{bmatrix}2&-1\\1&0\end{bmatrix} \quad\text{and}\quad S=\{\,m\in\mathbb{Z} : A^{m^2}+A^m=3I-A^{-6}\}.$$

Step 1: Notice that the characteristic equation of $A$ is

$$\det(A-\lambda I)=(\lambda-1)^2=0,$$

so $A$ has a single eigenvalue $\lambda=1$ with algebraic multiplicity 2. Hence, $A$ can be written as

$$A=I+N,\quad\text{with } N = A-I \text{ and } N^2=0.$$

Step 2: For any integer $k$,

$$A^k=(I+N)^k=I+kN \quad \text{(using the binomial expansion and } N^2=0\text{)}.$$

Step 3: Applying this to our equation:

$$A^{m^2} + A^m = \bigl[I + m^2N\bigr] + \bigl[I + mN\bigr] = 2I + (m^2+m)N.$$

Similarly,

$$A^{-6}=I+(-6)N=I-6N,$$

so

$$3I-A^{-6}=3I - (I-6N)=2I+6N.$$

Step 4: Equate the two expressions:

$$2I+(m^2+m)N = 2I+6N.$$

Comparing coefficients of $N$ (and noting $N \neq 0$), we have:

$$m^2+m =6.$$

This simplifies to:

$$m^2 + m - 6 =0 \quad \Rightarrow \quad (m+3)(m-2)=0.$$

Thus, the solutions are $m=-3$ and $m=2$.

Since $S=\{-3,\,2\}$, the number of elements is:

$$n(S)=2.$$

---

Minimal Explanation:

Write $A = I+N$ with $N^2 = 0$. Then $A^k = I+kN$. Substitute in the equation to get $2I+(m^2+m)N = 2I+6N$, which implies $m^2+m = 6$. Solve to obtain $m=-3,2$ and hence $n(S)=2$.