Question

Let $S$ be the set of all functions $f:[0,1] \to R$ , which are continuous on $[0,1]$ and differentiable on $(0,1).$ Then for every $f$ in $S$ , there exists a $c \in (0,1)$ , depending on $f$ , such that:
$1.\left| {f(c) - f(1)} \right| < (1 - c)\left| {f'(c)} \right| \\\ 2.\dfrac{{f(1) - f(c)}}{{1 - c}} = f'(c) \\\ 3.\left| {f(c) + f(1)} \right| < (1 + c)\left| {f'(c)} \right| \\\ 4.\left| {f(c) - f(1)} \right| < \left| {f'(c)} \right| \\\$

Answer 1

Hint : We will use Lagrange’s mean value theorem which states that if a function is differentiable on (0,1) and continuous on [0,1]. Then, there exists a c such that
$f'(c) = \dfrac{{f(1) - f(c)}}{{1 - c}}$ where $c \in (0,1)$ .
Now, using this theorem we will construct graphs and then interpret the values.

Complete step by step solution:
Case 1:
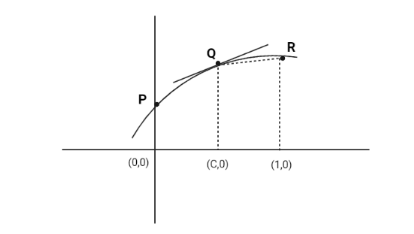
In the below image we see that,
$f'(c) >$ slope of $QR$
Now, we know that slope of QR is $\dfrac{{f(1) - f(c)}}{{1 - c}}$
Hence, $f'(c) > \dfrac{{f(1) - f(c)}}{{1 - c}}$
$\therefore (1 - c)\left| {f'(c)} \right| > \left| {f(c) - f(1)} \right|$

Now, In the below figure we see that the slope of $f'(c)$ and slope of QR is negative. But, the slope of $f'(c)$ is more negative than the slope of QR.

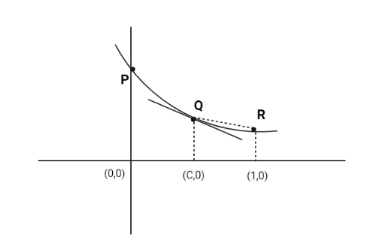
$\left| {f'(c)} \right| >$ | slope of QR|
we know that slope of QR is $\dfrac{{f(1) - f(c)}}{{1 - c}}$
$\therefore (1 - c)\left| {f'(c)} \right| > \left| {f(c) - f(1)} \right|$
From the above two graphs we conclude that
$(1 - c)\left| {f'(c)} \right| > \left| {f(c) - f(1)} \right|$
Case 2:
In the below image we see that,

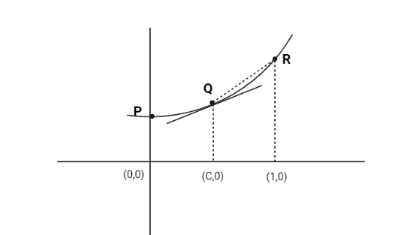
$f'(c) <$ slope of $QR$
Now, we know that slope of QR is $\dfrac{{f(1) - f(c)}}{{1 - c}}$
Hence, $f'(c) < \dfrac{{f(1) - f(c)}}{{1 - c}}$
$\therefore (1 - c)\left| {f'(c)} \right| < \left| {f(c) - f(1)} \right|$
Now, In the below figure we see that the slope of $f'(c)$ and slope of QR is negative. But, the slope of $f'(c)$ is less negative than the slope of QR.

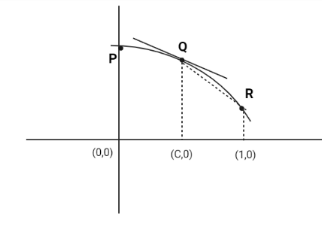
$\left| {f'(c)} \right| <$ | slope of QR|
we know that slope of QR is $\dfrac{{f(1) - f(c)}}{{1 - c}}$
$\therefore (1 - c)\left| {f'(c)} \right| < \left| {f(c) - f(1)} \right|$
From the above two graphs we conclude that
$(1 - c)\left| {f'(c)} \right| < \left| {f(c) - f(1)} \right|$
Now, from all the available options we see that option 1 matches with case 2.
Hence the correct option is 1.
So, the correct answer is “Option 1”.

Note : In the proof of the Fundamental Theorem of Calculus, the Mean Value Theorem plays a significant part. If f exists and is bounded on the interior and is continuous on $[a,b]$ , then f is of Bounded Variation on $[a,b]$ .