Question

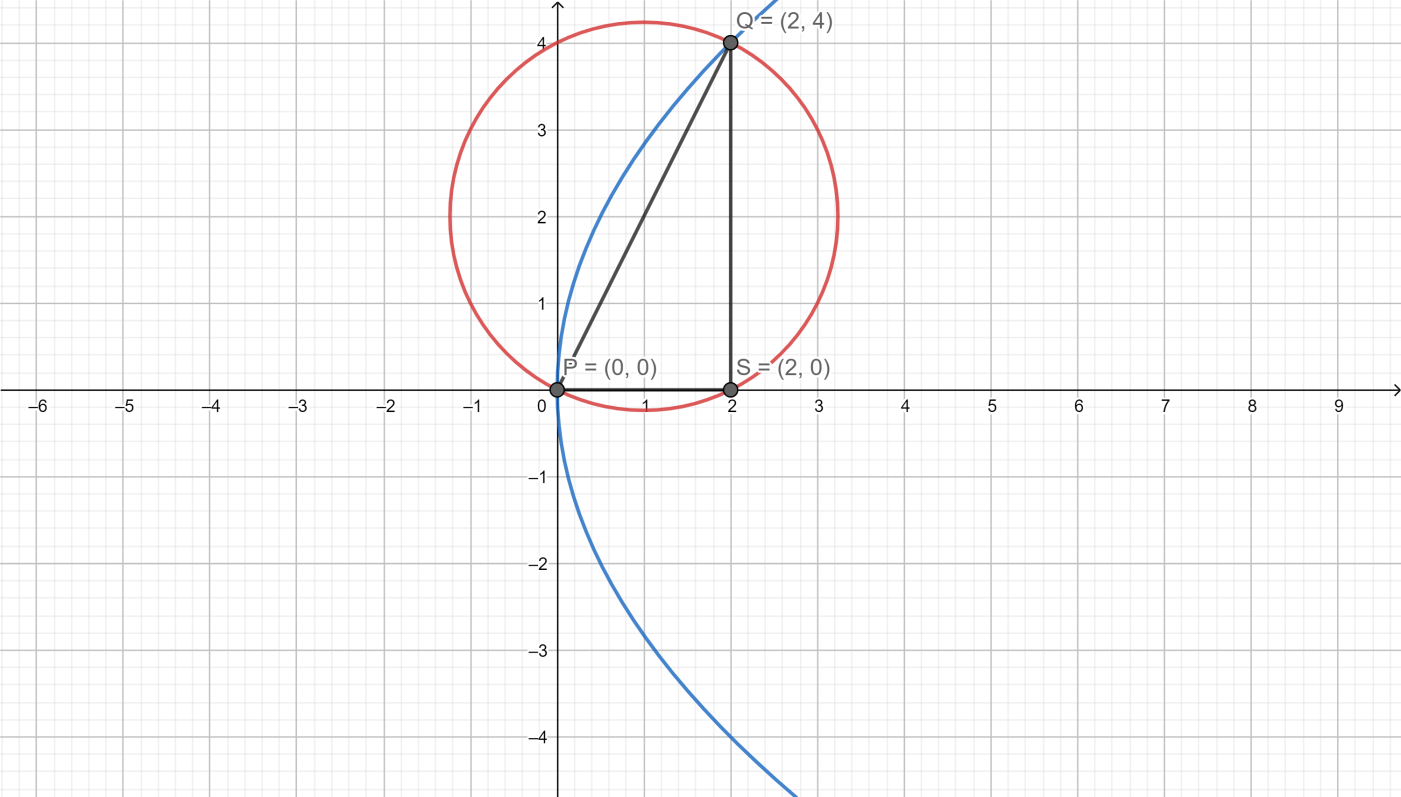
Let S be the focus of the parabola ${y^2} = 8x$ and PQ be the common chord of the circle ${x^2} + {y^2} - 2x - 4y = 0$ and the given parabola. The area of $\vartriangle PQS$ is
$\left( 1 \right)$ $6$ sq units
$\left( 2 \right)$ $16$ sq units
$\left( 3 \right)$ $4$ sq units
$\left( 4 \right)$ $64$ sq units

Answer 1

First compare the given equation of parabola with the general equation to find the value of $a$ .By this we will get the focus of the parabola. Put this value of $a$ in the general form of a point $P\left( {a{t^2},2at} \right)$ to get the value of $t$ .After getting the values of $t$ we are able to find both the vertices of points P and Q. These vertices P, Q and S make a triangle PQS then find the area of the triangle by using the formula.

Complete step-by-step solution:
As we know that if the directrix is parallel to the y-axis in the standard equation of a parabola then the equation of a parabola is given as
${y^2} = 4ax$ -------- (i)
Now in the question the equation of a parabola is given as
${y^2} = 8x$ -------- (ii)
On comparing the equations (i) and (ii) we get,
$4a = 8$
By shifting $4$ to the right hand side we get
$a = \dfrac{8}{4}$
On dividing $8$ by $4$ we get
$a = 2$ --------- (iii)
Because the focus of the parabola of equation ${y^2} = 4ax$ is given by $S\left( {a,0} \right)$ .Therefore, the focus of the parabola of equation ${y^2} = 8x$ will be $S\left( {2,0} \right)$ .
Let P be any point on the parabola which is given by $P\left( {a{t^2},2at} \right)$ .In the given question P is the one end of the common chord. So by putting the value of $a$ from the equation (iii) in this general form of point we get $P\left( {2{t^2},4t} \right)$ .
As it is given that PQ is the common chord of the circle ${x^2} + {y^2} - 2x - 4y = 0$ and the given parabola. That is P and Q are the common points of the circle and the parabola. So, we can say that the point $P\left( {2{t^2},4t} \right)$ satisfies the equation ${x^2} + {y^2} - 2x - 4y = 0$ .
So, put $x = 2{t^2}$ and $y = 4t$ in the given equation of the circle to find the value of $t$ .
$\Rightarrow {\left( {2{t^2}} \right)^2} + {\left( {4t} \right)^2} - 2\left( {2{t^2}} \right) - 4\left( {4t} \right) = 0$
On further solving we get
$\Rightarrow 4{t^4} + 16{t^2} - 4{t^2} - 16t = 0$
On subtracting ${t^2}$ terms we get
$\Rightarrow 4{t^4} + 12{t^2} - 16t = 0$
Taking $4t$ common from the above expression we get
$\Rightarrow 4t\left[ {{t^3} + 3t - 4} \right] = 0$
So from this we have
$4t = 0$ and ${t^3} + 3t - 4 = 0$
On Solving the equation $4t = 0$ we get $t = 0$
Since the constant in the equation ${t^3} + 3t - 4 = 0$ is $4$ ,that is the integer root must be a factor of $4$ .The possible values are $\pm 1$ , $\pm 2$ and $\pm 4$ .Now test these values by substituting them in the equation ${t^3} + 3t - 4 = 0$ .
At $t = 1$ , ${\left( 1 \right)^3} + 3\left( 1 \right) - 4 = 0$
$\Rightarrow 4 - 4 = 0$
$\Rightarrow 0 = 0$
So, that means $t = 1$ satisfies the equation. Similarly you can check for rest of the possible values by substituting them in the equation. But at last you will find that $t = 1$ is the only value which satisfies the equation because of the absence of ${t^2}$ term.
Hence the required values of $t$ are $0$ and $1$ . Now put these values in the point P.
At $t = 0$ , we get one point as $P\left( {0,0} \right)$ and
At $t = 1$ , we get another point as $Q\left( {2,4} \right)$
Now we have a total of three points which makes a triangle PQS. So to find the area of this triangle will use the formula by which we can find the area of the triangle with the help of vertices. Let first talk in general, If $A\left( {{x_1},{y_1}} \right)$ , $B\left( {{x_2},{y_2}} \right)$ and $C\left( {{x_3},{y_3}} \right)$ be the three vertices of the triangle ABC then
Area of $\vartriangle$ $= \left| {\dfrac{1}{2}\left[ {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)} \right]} \right|$
In this question we have to find the area of $\vartriangle PQS$ where the three vertices are $P\left( {0,0} \right)$ , $Q\left( {2,4} \right)$ and $S\left( {2,0} \right)$ .Therefore,
Area of $\vartriangle PQS$ $= \left| {\dfrac{1}{2}\left[ {0\left( {4 - 0} \right) + 2\left( {0 - 0} \right) + 2\left( {0 - 4} \right)} \right]} \right|$
On further solving we get
Area of $\vartriangle PQS$ $= \left| {\dfrac{1}{2}\left[ {0 + 0 - 8} \right]} \right|$
By dividing $8$ by $2$ we get
Area of $\vartriangle PQS$ $= \left| { - 4} \right|$
Therefore, the area of $\vartriangle PQS$ is $4$ sq units.
Hence the correct option is $\left( 3 \right)$ $4$ sq units

Note: Keep in mind that area can never be negative, area is always positive. Remember that the focus of the parabola of equation ${y^2} = 4ax$ is given by $S\left( {a,0} \right)$. Remember that any point on the parabola is given by $\left( {a{t^2},2at} \right)$ .Make sure that you do not make any mistake while substituting the values in the formula to find the area of the triangle.