Question
Question: Let S be the area of the region enclosed by \(y = {e^{ - {x^2}}},y = 0,x = 0,x = 1.\) Then, A) \(S...
Let S be the area of the region enclosed by y=e−x2,y=0,x=0,x=1. Then,
A) S⩾e1
B) S⩾1−e1
C) S⩽41(1+e1)
D) S⩽21+e1(1−21)
Solution
First we have to draw the figure and understand the area S. Then the first two options can be checked simply using the values of x,y. Using B, C can be checked. Certain rearrangements are needed to check D. The concept used here is that the area under a curve is equal to the integral value. For applying this we have to find the limits as well.
Formula used:
Area enclosed by a curve y=f(x) within the limits x=a to x=b is simply the integral of the curve with same limits.
⇒S=a∫bf(x)dx
Complete step by step answer:
Given that S is the area enclosed by y=e−x2,y=0,x=0,x=1.
y=0,x=0 represent the x,y axis respectively.
Let the curve drawn represent y=e−x2.
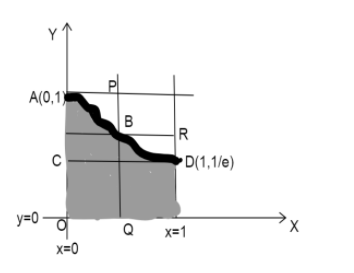
In the figure, the shaded portion represents the area S.
When x=1⇒y=e−x2=e−1=e1.
Since S contains a rectangle OSDC with vertices (0,0),(1,0),(1,e1),(0,e1), where S(1,0).
The area of that rectangle will be A=length×breadth
⇒A=1×e1=e1.
Therefore clearly S⩾e1.
This implies option A is right.
Also, since S is the area enclosed by the curve y=e−x2,x=0,y=0,x=1
We can consider S=0∫1e−x2dx.
⇒x∈[0,1]⇒x2⩽x
Multiplying both sides by −1 and taking exponents we have,
⇒−x2⩾−x⇒e−x2⩾e−x
Therefore, S=0∫1e−x2dx⩾0∫1e−xdx
Integrating we get, S⩾[−e−x]01=e0−e−1=1−e1
⇒S⩾1−e1
Therefore option B is also right.
To show that option C is incorrect,
⇒e>e⇒e1<e1
⇒−e1<e1⇒1−e1<1+e1<41(1+e1)
This implies 1−e1<41(1+e1)
From B, we have S⩾1−e1
Using these two equations we can say C is incorrect.
Moving on, consider two rectangles in the figure OAPQ and QBRS where S(1,0),
Clearly S⩽ Area of OAPQ+ Area of QBRS
PQ is drawn parallel to Y axis at the point x=21.
Then y=e−x2=e−21=e1.
Therefore, B is the point (21,e1).
Area of OAPQ =lenth×breadth=1×21=21
In QBRS, QB=e1,BR=1−21
Therefore, Area of QBRS =length×breadth=e1×1−21
⇒S⩽AreaOAPQ+AreaQBRS=21+e1(1−21)
So, option D is correct.
Therefore, Option (A), (B) and (D) are correct.
Note:
It is important to identify the graph of the given function and mark the given region. If there is some portion under the X-axis, this area will be negative. So be careful in those cases to split the region if necessary and find the area separately.
