Question

Let S be a set of all points in $\left( -\pi ,\pi \right)$, at which the function f\left( x \right)=\min \left\\{ \sin x,\cos x \right\\} is not differentiable. Then S is a subset of which of the following?
\begin{aligned} & \left( A \right)\left\\{ -\dfrac{3\pi }{4},\dfrac{\pi }{4} \right\\} \\\ & \left( B \right)\left\\{ -\dfrac{3\pi }{4},\dfrac{\pi }{2},\dfrac{3\pi }{4} \right\\} \\\ & \left( C \right)\left\\{ -\dfrac{\pi }{2},-\dfrac{\pi }{4},\dfrac{\pi }{4},\dfrac{\pi }{2} \right\\} \\\ & \left( D \right)\left\\{ -\dfrac{\pi }{4},0,\dfrac{\pi }{4} \right\\} \\\ \end{aligned}

Answer 1

We start solving this problem by going through the definition of differentiability and we plot the graphs of $\sin x$ and $\cos x$ and find the regions where they are minimum and we plot the curve for $f\left( x \right)$. Then we find the points where the graph has breaks to find the points where the function is not differentiable.

Complete step-by-step solution:
First, let us go through the concept of differentiability.
Any function $f\left( x \right)$ is said to be differentiable if a tangent exists to the curve at that point, so the graph of the curve should be relatively smooth and cannot contain any break.
Now, let us look at the graph of the curves of $\sin x$ (orange) and $\cos x$ (red).

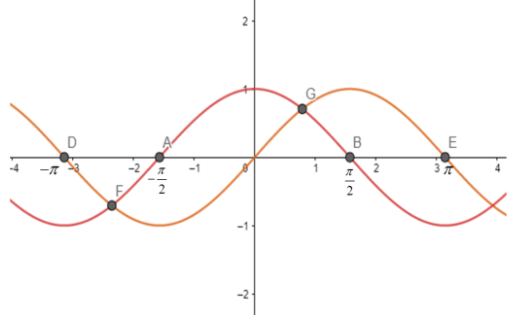
Now, as we need the graph for the function f\left( x \right)=\min \left\\{ \sin x,\cos x \right\\}, let us look at the above graph to find the region where $\sin x$ is minimum and where $\cos x$ is minimum.
In the region $\left( -\pi ,\pi \right)$, cosx is minimum in region $\left( -\pi ,\dfrac{3\pi }{4} \right)$ and $\left( \dfrac{\pi }{4},\pi \right)$ and sinx is minimum in the region $\left( -\dfrac{3\pi }{4},\dfrac{\pi }{4} \right)$.
So now let us plot the graph for f\left( x \right)=\min \left\\{ \sin x,\cos x \right\\}.

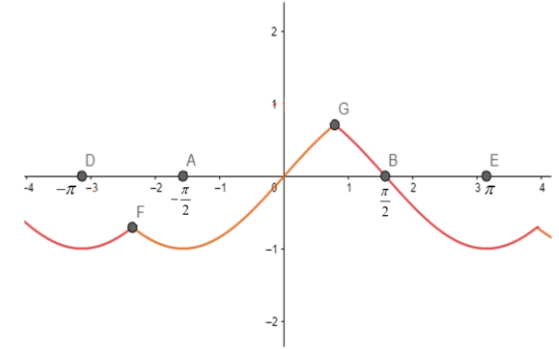
Now from the above graph let us find the points where the curve has breaks or cusps.
We can see that the curve has rough edges at the points where $x=\dfrac{\pi }{4}$ and $x=-\dfrac{3\pi }{4}$ in the region $\left( -\pi ,\pi \right)$.
Hence the function $f\left( x \right)$ is not differentiable at points \left\\{ -\dfrac{3\pi }{4},\dfrac{\pi }{4} \right\\}.
So, S=\left\\{ -\dfrac{3\pi }{4},\dfrac{\pi }{4} \right\\}.
As any set is subset of itself, our answer is S=\left\\{ -\dfrac{3\pi }{4},\dfrac{\pi }{4} \right\\}.
Hence, the answer is Option A.

Note: We can also find the points of discontinuity by checking as below
First let us find the points where sinx is minimum.
$\begin{aligned} & \Rightarrow \sin x<\cos x \\\ & \Rightarrow \tan x<1 \\\ & \Rightarrow x\in \left( -\dfrac{3\pi }{4},\dfrac{\pi }{4} \right) \\\ \end{aligned}$
Then we find the region where cosx is minimum.
$\begin{aligned} & \Rightarrow \cos x<\sin x \\\ & \Rightarrow \tan x>1 \\\ & \Rightarrow x\in \left( -\pi ,-\dfrac{3\pi }{4} \right)\cup \left( \dfrac{\pi }{4},\pi \right) \\\ \end{aligned}$
Then we plot the graph as we have done in the solution part and find the points of discontinuity.