Question

Let S and S' be the foci of the ellipse and B be any one of the extremities of its minor axis. If $\vartriangle {S'}BS$ is a right angled triangle with right angle at $B$ and $area\left( {\vartriangle {S'}BS} \right) = 8{\text{ sq}}{\text{. units}}$ , then the length of a latus rectum of the ellipse is:
(A) $2\sqrt 2$
(B) $2$
(C) $4$
(D) $4\sqrt 2$

Answer 1

We will first find the coordinates of $S'$ , $S$ and $B$ , then the equation of lines ${S'}B$ and $SB$ . Using the property of perpendicular lines and equating the product of slopes of lines ${S'}B$ and $SB$ to $- 1$ and we will find the value of eccentricity, relation between length of major and minor axis and then using this relation we will find the area of $\vartriangle {S'}BS$ in terms of major and minor axis and then finally equate it to the given area to find the value of major and major axis and putting these values in formula to find the length of the latus rectum, will give the length

Complete step-by-step solution:

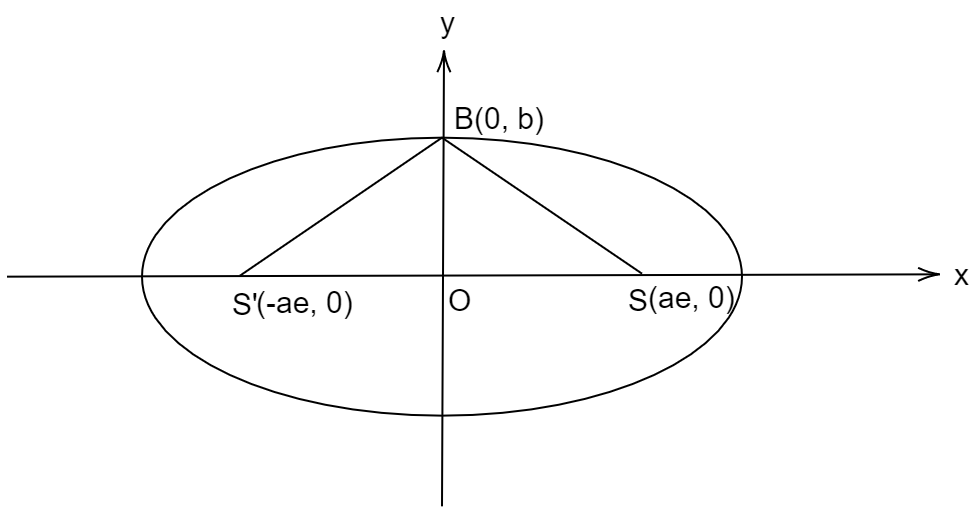
Let the length of the major axis be $2a$ and length of the minor axis be $2b$ .
We know that for a standard ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ , foci of ellipse is given by ${S'}\left( { - ae,0} \right)$ and $S\left( {ae,0} \right)$ where, $a$ is half the length of major axis and $e$ is the eccentricity of the ellipse.
Since the point $B$ lies on the y-axis its coordinate will be $(0,b)$ as shown in figure.
Slope ($m$) of a line is given by
$m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
Therefore, slope of line ${S'}B$ (${m_1}$)$= \dfrac{{b - 0}}{{0 - \left( { - ae} \right)}}$
$\Rightarrow {m_1} = \dfrac{b}{{ae}}$
Similarly, slope of line $SB$(${m_2}$) $= \dfrac{{b - 0}}{{0 - ae}}$
$\Rightarrow {m_2} = - \dfrac{b}{{ae}}$
We know that if two lines are perpendicular then the product of their slopes is $- 1$ .
Given, $\vartriangle {S'}BS$ is a right angled triangle with right angle at $B$ , so
$\Rightarrow {m_1} \times {m_2} = - 1$
Putting the values of ${m_1}$ and ${m_2}$ ,
$\Rightarrow \left( {\dfrac{b}{{ae}}} \right) \times \left( {\dfrac{{ - b}}{{ae}}} \right) = - 1$
On multiplying,
$\Rightarrow - \dfrac{{{b^2}}}{{{a^2}{e^2}}} = - 1$
$\Rightarrow \dfrac{{{b^2}}}{{{a^2}{e^2}}} = 1$
Taking ${a^2}{e^2}$ to R.H.S.
$\Rightarrow {b^2} = {a^2}{e^2} - - - (1)$
Also, we know for ellipse
$e = \sqrt {1 - {{\left( {\dfrac{b}{a}} \right)}^2}}$
On squaring both sides,
${e^2} = 1 - \dfrac{{{b^2}}}{{{a^2}}}$
On rearranging,
$\Rightarrow {a^2}{e^2} = {a^2} - {b^2}$
$\Rightarrow {a^2}{e^2} - {a^2} = {b^2}$
Taking ${a^2}$ common from L.H.S.
$\Rightarrow {a^2}(1 - {e^2}) = {b^2} - - - (2)$
On comparing $(1)$ and $(2)$ ,
$\Rightarrow {a^2}{e^2} = {a^2}\left( {1 - {e^2}} \right)$
Dividing both sides by ${a^2}$ ,
$\Rightarrow {e^2} = \left( {1 - {e^2}} \right)$
On solving,
$\Rightarrow 2{e^2} = 1$
Dividing both sides by $2$ ,
$\Rightarrow {e^2} = \dfrac{1}{2}$
$\therefore e = \dfrac{1}{{\sqrt 2 }}$
Putting the value of ${e^2}$ in $(1)$ ,
$\Rightarrow {b^2} = \dfrac{{{a^2}}}{2} - - - (3)$
Now, we know area of a right triangle $= \dfrac{1}{2} \times {\text{Base}} \times {\text{Height}}$
Here, the base is $2ae$ and height is $b$ .
Also given, $area\left( {\vartriangle {S'}BS} \right) = 8{\text{ sq}}{\text{. units}}$.
$\Rightarrow \dfrac{1}{2} \times \left( {2ae} \right) \times b = 8$
Putting the value of $e$ and on solving
$\Rightarrow ab = 8\sqrt 2$
On squaring both the sides,
$\Rightarrow {a^2}{b^2} = 64 \times 2$
Using $(3)$ ,
$\Rightarrow {a^2} \times \dfrac{{{a^2}}}{2} = 64 \times 2$
On rewriting,
$\Rightarrow {a^4} = {\left( 4 \right)^4}$
$\therefore a = 4$
Putting the value of $a$ in $(3)$ ,
$\Rightarrow {b^2} = \dfrac{{{{\left( 4 \right)}^2}}}{2}$
$\therefore {b^2} = 8$
Length of latus rectum $= \dfrac{{2{b^2}}}{a}$
$= \dfrac{{2 \times 8}}{4}$
$= 4$
Therefore, the length of a latus rectum of the ellipse is $4$ .
Hence, option (C) is correct.

Note: In this question the most important thing to keep in mind is the coordinates of foci, formula for eccentricity of ellipse, area of right angle triangle and formula to find the length of the latus rectum. One should keep in mind that foci of an ellipse are equidistant from origin and also that the product of slopes of two perpendicular lines is equal to $- 1$ .