Question

Let ${{S}_{1}}$ and ${{S}_{2}}$ be the foci of the ellipse
$\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{8}=1$. If $A\left( x,y \right)$ is any point on the ellipse, then the maximum area of the $\Delta A{{S}_{1}}{{S}_{2}}$ (in sq. units) is:
F. $2\sqrt{2}$
G. $2\sqrt{3}$
H. $8$
I. $4$
J. $16$

Answer 1

To find the area, we need to first find the eccentricity of the ellipse and after finding the eccentricity of the ellipse we will find the maximum area formed by a triangle of $\Delta A{{S}_{1}}{{S}_{2}}$ by taking $\Delta A$ as $\left( x,y \right)$ using the formula as:
Maximum Area $=\dfrac{1}{2}\left( SS' \right)\times \text{Max}\text{. value of }A$ and eccentricity of the ellipse is given as:
$e=\sqrt{\dfrac{{{a}^{2}}-{{b}^{2}}}{{{a}^{2}}}}$ where $a,b$ are given in the ellipse as
$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$.

Complete step by step solution:
According to the question given, the equation for the ellipse is given as
$\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{8}=1$ and to find the maximum area of a triangle formed inside the ellipse we first draw a triangle with ellipse diagram as shown below:

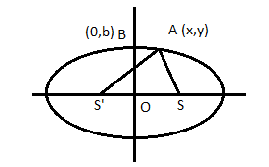
Now to find the value of A$\left( x,y \right)$ we will see as to where on the ellipse if the tip of the triangle be placed so as to get the value of the coordinates of A now the points ${{S}_{1}}$ and ${{S}_{2}}$ as foci the distance ${{S}_{1}}O$ and ${{S}_{2}}O$ are equal therefore, the maximum coordinates of A that can form the maximum area of the triangle.
Now we need to find the value of b and to find the value of b, we put the ellipse equation as:
$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ and placing it with
$\dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{8}=1$ we get the value of a,b as :
$\Rightarrow {{a}^{2}}=16,{{b}^{2}}=8$
$\Rightarrow a=\sqrt{16},b=\sqrt{8}$
$\Rightarrow a=4,b=2\sqrt{2}$
Hence, the coordinate of A is$\left( 0,2\sqrt{2} \right)$.
Now we need to find the length of ${{S}_{1}}O$ and ${{S}_{2}}O$ and the length of these two parts are $ae$. The term e is the eccentricity whose formula is $e=\sqrt{\dfrac{{{a}^{2}}-{{b}^{2}}}{{{a}^{2}}}}$.
Now finding the value of e as:
$\Rightarrow e=\sqrt{\dfrac{{{a}^{2}}-{{b}^{2}}}{{{a}^{2}}}}$
$\Rightarrow e=\sqrt{\dfrac{16-8}{16}}$
$\Rightarrow e=\dfrac{1}{\sqrt{2}}$
Hence, the foci length $\left( SO=S'O \right)$ of the ellipse is given as $ae$ which is equal to $4\times \dfrac{1}{\sqrt{2}}=\dfrac{4}{\sqrt{2}}$.
Now to find the area of the triangle $\Delta A{{S}_{1}}{{S}_{2}}$ we use the formula as:
$\Rightarrow \dfrac{1}{2}\left( SS' \right)\times b$
And placing the values in the above formula, we get the area of the triangle as:
$\Rightarrow \dfrac{1}{2}\left( SO+S'O \right)\times b$
$\Rightarrow \dfrac{1}{2}\times 2\dfrac{4}{\sqrt{2}}\times 2\sqrt{2}$
$\Rightarrow 8$ unit square
Therefore, the area of the triangle inside the ellipse is $8$ unit square.

Note: Foci is the plural of focus and eccentricity is the conical section of the ellipse when folded, the value of eccentricity for parabola is equal to 1, for ellipse it is less than 1 and for hyperbola it is greater than 1.