Question

Let ${{S}_{1}}=0$ and ${{S}_{2}}=0$ be two circles intersecting at P(6,4) and both arc tangent to x-axis and y=mx (where m>0). If product of radii of the circles ${{S}_{1}}=0$ and ${{S}_{2}}=0$ is $\dfrac{52}{3}$​. Then find the value of m.

Answer 1

Hint: To solve this question where two circles ${{S}_{1}}=0$ and ${{S}_{2}}=0$ are involved we will go for assuming the coordinates of the centre of the circle and similarly the radius of the circle. And after doing so we will go for the necessary calculations to find the result.

Complete step-by-step solution -

Consider the first circle ${{S}_{1}}=0$.
Because the circle ${{S}_{1}}=0$ touches the x axis therefore the coordinate of the centre of the circle would be given by x coordinate as some number h and the y coordinate would be equal to the radius of the circle.
We will now draw the figure of the situation. The figure is given as,

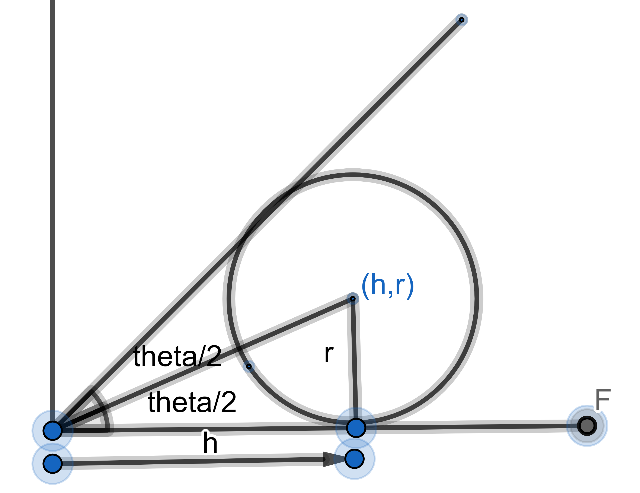
On the similar argument let the centre of the circle be (h,r), where r is the radius of the first circle ${{S}_{1}}=0$ as it touches the x-axis.
Therefore, the equation of circle ${{S}_{1}}=0$ is given by,
${{\left( x-h \right)}^{2}}+{{\left( y-r \right)}^{2}}={{r}^{2}}.........(i)$
This circle also touches y=mx.

Let $m=tan\theta$ (where $\theta$ is an angle made with x-axis).
Now observing the figure, we get that,

& tan\left( \dfrac{\theta }{2} \right)=\dfrac{r}{h} \\\ & \Rightarrow r=h\tan\left( \dfrac{\theta }{2} \right) \\\ & \Rightarrow h=r\cot \left( \dfrac{\theta }{2} \right) \\\ \end{aligned}$$ Putting the above obtained value of h in equation (i) we get, $$\Rightarrow {{(x-rcot\dfrac{\theta }{2})}^{2}}+{{(y-r)}^{2}}={{r}^{2}}$$. Now as both circles pass through (6,4). Therefore, putting value of x as 6 and y as 4 in above equation we get, $$\Rightarrow {{(6-rcot\dfrac{\theta }{2})}^{2}}+{{(4-r)}^{2}}={{r}^{2}}$$ The above obtained equation is a quadratic equation in r, hence gives two values of the radius r. Two values of r give the radius of two possible circles whose product is given to be $$\dfrac{52}{3}$$. Solving the above we get, $$\begin{aligned} & 36+{{r}^{2}}co{{t}^{2}}\left( \dfrac{\theta }{2} \right)-12rcot\left( \dfrac{\theta }{2} \right)+16{{r}^{2}}-8r={{r}^{2}} \\\ & \Rightarrow {{r}^{2}}co{{t}^{2}}\left( \dfrac{\theta }{2} \right)+r(-12cot\left( \dfrac{\theta }{2} \right)-8)+52=0 \\\ \end{aligned}$$ Product of two roots of the above equation is given as $$\dfrac{52}{3}$$. Product of the roots is given by $$\dfrac{c}{a}$$, Here we have $$a=co{{t}^{2}}\left( \dfrac{\theta }{2} \right)$$ and c = 52. ​ $$\begin{array}{*{35}{l}} \dfrac{c}{a}=\dfrac{52}{3} \\\ \Rightarrow 52co{{t}^{2}}\left( \dfrac{\theta }{2} \right)=\dfrac{52}{3} \\\ \Rightarrow co{{t}^{2}}\left( \dfrac{\theta }{2} \right)=3 \\\ \Rightarrow ta{{n}^{2}}\left( \dfrac{\theta }{2} \right)=\dfrac{1}{3} \\\ tan\left( \dfrac{\theta }{2} \right)=\pm \dfrac{1}{\sqrt{3}} \\\ \Rightarrow tan\left( \dfrac{\theta }{2} \right)=\dfrac{1}{\sqrt{3}} \\\ \end{array}$$ Since the Circle is in the first quadrant therefore tan is positive. (∵ Taking x-axis and passing through (6,4)) $$\begin{aligned} & \Rightarrow \dfrac{\theta }{2}=\dfrac{\pi }{6} \\\ & \Rightarrow \theta =\dfrac{\pi }{3} \\\ \end{aligned}$$ Therefore, we got, $$\begin{aligned} & \tan \theta =\sqrt{3} \\\ & \Rightarrow m=\sqrt{3} \\\ \end{aligned}$$ Hence, we obtain the value of m as $$\sqrt{3}$$ Note: The possibility of error in these types of question can be at a point where you can mistakenly take the value of tan as negative. Always first check for the quadrant in which calculations are done and then go for taking positive or negative signs of trigonometric functions.