Question

Let RS be the diameter of the circle ${x^2} + {y^2} = 1$, where S is the point $(1,0)$. Let P be a variable point (other than R and S) on the circle and tangents to the circle at S and P meet at the point Q. The normal to the circle at P intersects a line drawn through Q parallel to RS at point E. Then the locus of E passes through the point(s)
A. $\left( {\dfrac{1}{3},\dfrac{1}{{\sqrt 3 }}} \right)$
B. $\left( {\dfrac{1}{4},\dfrac{1}{2}} \right)$
C. $\left( {\dfrac{1}{3},\dfrac{{ - 1}}{{\sqrt 3 }}} \right)$
D. $\left( {\dfrac{1}{4},\dfrac{{ - 1}}{2}} \right)$

Answer 1

First of all this a simple problem, though it may seem to be complex. In order to solve the problem, we need to have some knowledge regarding a few topics about circles. Such as the basic general equation form of a circle, tangent equation of a circle. When given the equation of a circle, we should be able to recognize the coordinates of the center and the radius of the circle.

Complete answer:
The general equation form of a circle is given by ${x^2} + {y^2} = {r^2}$, where the center of the circle is the origin and it has a radius of r units.
Visualizing the given information inform in a figure, as given below:
Given that the circle is of a radius of 1 unit, from ${x^2} + {y^2} = 1$, from here it is clear that the radius of the circle is 1 unit.

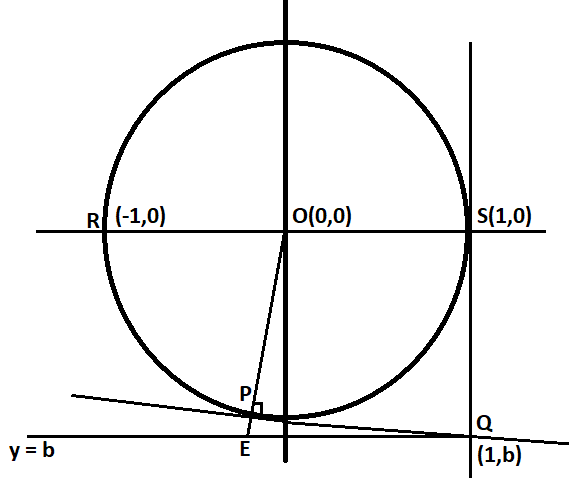
Gathering from the given information, P is a point on the tangent of the circle.
The tangents drawn from these points S and P meet at Q, which is a point on the same vertical line as the point S, which means that the x-coordinate remains the same for the point Q, which is 1.
The x-coordinate for Q is 1, and let the y-coordinate be a variable b.
So the coordinates of the point are $Q{\text{ }} = \left( {1,b} \right)$
A normal of the circle or the tangent passes through its center, hence here the normal to the circle through the point P, intersects a line drawn through Q parallel to RS at point E.
Now the line parallel to RS which is the line QE, as it passes through the point Q and parallel to RS, which means that Q and E are on the same horizontal line, which means that the points Q and E have the same y-coordinate which is b.
Let us consider the coordinates of the point P to be $\left( {\cos \theta ,\sin \theta } \right)$, as P is the point on the circle it should satisfy the circle equation which is ${x^2} + {y^2} = 1$, so x-coordinate to be $\cos \theta$and y-coordinate to be $\sin \theta$satisfies the equation${x^2} + {y^2} = 1$.
$\Rightarrow {\cos ^2}\theta + {\sin ^2}\theta = 1$
Now as this normal line OP passes through the origin and the point $P(\cos \theta ,\sin \theta )$.
Hence the equation of any line which passes through the origin is given by $y = mx$
Here m is the slope of the line OP, which is given by the ratio of difference of y coordinates to the difference of x coordinates of $O\left( {0,0} \right)$ and $P(\cos \theta ,\sin \theta )$, as given below:
$\Rightarrow m = \dfrac{{\sin \theta - 0}}{{\cos \theta - 0}}$
$\Rightarrow m = \tan \theta$
Hence the equation of the line OP is given by:
$\Rightarrow y = \left( {\tan \theta } \right)x$
This line OP also passes through the point E, hence this point should satisfy the equation $y = \left( {\tan \theta } \right)x$.
We only the y-coordinate of the point E which is b, so by substituting the y-coordinate in the equation$y = \left( {\tan \theta } \right)x$, gives:
$\Rightarrow b = \left( {\tan \theta } \right)x$
$\Rightarrow \dfrac{b}{{\tan \theta }} = x$, is the x-coordinate of the point E
$\therefore$The coordinates of the point E are $\left( {\dfrac{b}{{\tan \theta }},b} \right)$.
We know that the tangent equation of the circle is given by:
$\Rightarrow x{x_1} + y{y_1} = {r^2}$
Where r is the radius of the circle and $\left( {{x_1},{y_1}} \right)$are the coordinates of the point on the circle and the tangent of the circle, which is P here, as given below:
$\Rightarrow \left( {{x_1},{y_1}} \right) = \left( {\cos \theta ,\sin \theta } \right)$
Hence the tangent equation becomes:
$\Rightarrow x\cos \theta + y\sin \theta = 1$
This tangent meets the point $Q{\text{ }}\left( {1,b} \right)$, therefore this point should satisfy the tangent equation as given below:
$\Rightarrow 1\left( {\cos \theta } \right) + b\left( {\sin \theta } \right) = 1$
$\Rightarrow \cos \theta + b\sin \theta = 1$
On expanding $\cos \theta$ and $\sin \theta$, as given below:
$\Rightarrow \left( {1 - 2{{\sin }^2}\dfrac{\theta }{2}} \right) + b\left( {2\sin \dfrac{\theta }{2}\cos \dfrac{\theta }{2}} \right) = 1$
$\Rightarrow 1 - 2{\sin ^2}\dfrac{\theta }{2} + 2b\sin \dfrac{\theta }{2}\cos \dfrac{\theta }{2} = 1$
As 1 gets cancelled on both sides, as given below:
$\Rightarrow 2{\sin ^2}\dfrac{\theta }{2} = 2b\sin \dfrac{\theta }{2}\cos \dfrac{\theta }{2}$
The above expression is obtained after $2\sin \dfrac{\theta }{2}$ gets cancelled on both sides.
$\Rightarrow \sin \dfrac{\theta }{2} = b\cos \dfrac{\theta }{2}$
$\Rightarrow \dfrac{{\sin \dfrac{\theta }{2}}}{{\cos \dfrac{\theta }{2}}} = b$
$\therefore b = \tan \dfrac{\theta }{2}$
Now substituting the value of b in the point $E\left( {\dfrac{b}{{\tan \theta }},b} \right)$
The x-coordinate of E is $\dfrac{b}{{\tan \theta }} = \dfrac{{\tan \dfrac{\theta }{2}}}{{\tan \theta }}$,
The y-coordinate of E is $b = \tan \dfrac{\theta }{2}$
Expanding the x-coordinate, as given below:
$\Rightarrow \dfrac{{\tan \dfrac{\theta }{2}}}{{\tan \theta }} = \dfrac{{\tan \dfrac{\theta }{2}}}{{\dfrac{{2\tan \dfrac{\theta }{2}}}{{1 - {{\tan }^2}\dfrac{\theta }{2}}}}}$
$\Rightarrow \dfrac{{\tan \dfrac{\theta }{2}}}{{\tan \theta }} = \dfrac{1}{2}\left( {1 - {{\tan }^2}\dfrac{\theta }{2}} \right)$
$\therefore x = \dfrac{1}{2}\left( {1 - {{\tan }^2}\dfrac{\theta }{2}} \right)$
And $y = \tan \dfrac{\theta }{2}$
Hence the locus of the point E is ${y^2} + 2x = 1$
We can verify this by substitution as given below:
$\Rightarrow {y^2} + 2x = {\left( {\tan \dfrac{\theta }{2}} \right)^2} + 2\left( {\dfrac{1}{2}\left( {1 - {{\tan }^2}\dfrac{\theta }{2}} \right)} \right)$
$\Rightarrow {y^2} + 2x = {\tan ^2}\dfrac{\theta }{2} + 1 - {\tan ^2}\dfrac{\theta }{2}$
$\Rightarrow {y^2} + 2x = 1$
$\therefore {y^2} + 2x = 1$ is the locus of the point E.

Hence the locus of the point E passes only through $\left( {\dfrac{1}{3},\dfrac{1}{{\sqrt 3 }}} \right)$ and $\left( {\dfrac{1}{3},\dfrac{{ - 1}}{{\sqrt 3 }}} \right)$

Note:
There is one important thing which we have to understand is that we know that the general equation of a circle is given by ${x^2} + {y^2} = 1$, where the circle center is (0,0) and the radius of the circle is 1 unit. Whereas if given the circle equation as ${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}$, then the center of the circle is (a,b) and the radius of the circle is r units. Also the trigonometric formulas were used like $\cos \theta = 1 - 2{\sin ^2}\dfrac{\theta }{2}$ and $\sin \theta = 2\sin \dfrac{\theta }{2}\cos \dfrac{\theta }{2}$, which are very important to remember.