Question

Let, $\rho \left( r \right) = \dfrac{{Qr}}{{\pi {R^4}}}$ be the charge density distribution for a solid sphere of radius $R$ and the total charge $Q$ . For a point $P$ inside the sphere at a distance ${r_1}$ from the centre of the sphere, the magnitude of electric field is:
(A) $\dfrac{Q}{{4\pi {\varepsilon _0}r_1^2}}$
(B) $\dfrac{{Q_1^2r_1^2}}{{4\pi {\varepsilon _0}{R^4}}}$
(C) $\dfrac{{Q_1^2}}{{3\pi {\varepsilon _0}{R^4}}}$
(D) Zero

Answer 1

First of all, we will find the small area element by using the formula of the area of the sphere. Then we will take the small electric field into account. To find the net or total electric field, we will integrate over the whole sphere. We will manipulate accordingly and obtain the result.

Complete step by step solution:
To begin with, let us first draw a diagram according to the condition given in the question.

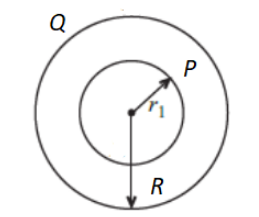
From the diagram, we can say that a point $P$ is located inside the sphere at a distance ${r_1}$ from the centre of the sphere. The radius of the sphere is $R$ and the charge enclosed by it is $Q$ .To proceed further, let us consider a differential thickness of $dr$ at the radius of $r$.Then the area of the differential element can be written as:
$dA = 4\pi {r^2}dr$ …… (1)
Where,
$dA$ indicates the small area.
$r$ indicates the radius of the part.
$dr$ indicates the differential thickness.
Now, we write the expression which gives the differential electric field as:
$dE = \dfrac{{kdQ}}{{r_1^2}}$ …… (2)
Where,
$dE$ indicates the differential electric field.
$k$ indicates a constant whose value is$\dfrac{1}{{4\pi {\varepsilon _0}}}$ .
$dQ$ indicates the small charge.
We can modify the equation (2) as follows:
$dE = \dfrac{{kdQ}}{{r_1^2dA}} \times dA \\\ \Rightarrow dE = \dfrac{k}{{r_1^2}} \times \dfrac{{dQ}}{{dA}} \times 4\pi {r^2}dr$
But, $\dfrac{{dQ}}{{dA}}$ is the charge distribution density whose values is given as $\dfrac{{Qr}}{{\pi {R^4}}}$.
So, we can write:
dE = \dfrac{k}{{r_1^2}} \times \dfrac{{Qr}}{{\pi {R^4}}} \times 4\pi {r^2}dr \\\ \Rightarrow \int {dE = \int {\dfrac{k}{{r_1^2}} \times \dfrac{{Qr}}{{\pi {R^4}}} \times 4\pi {r^2}dr} } \\\ \Rightarrow E = \dfrac{Q}{{4\pi {\varepsilon _0}r_1^2\pi {R^4}}}\int\limits_0^{{r_1}} {4\pi {r^3}dr} \\\ \Rightarrow E = \dfrac{Q}{{4\pi {\varepsilon _0}r_1^2\pi {R^4}}} \times 4\pi \left[ {\dfrac{{{r^4}}}{4}} \right]_0^{{r_1}} \\\
Again, we manipulate further, and we get:
$\Rightarrow E = \dfrac{Q}{{4\pi {\varepsilon _0}r_1^2\pi {R^4}}} \times 4\pi \times \dfrac{{r_1^4}}{4} \\\ \therefore E = \dfrac{{Qr_1^2}}{{4\pi {\varepsilon _0}{R^4}}}$
Hence, the magnitude of the electric field is $\dfrac{{Qr_1^2}}{{4\pi {\varepsilon _0}{R^4}}}$.

The correct option is (B).

Note: This problem can be solved if you have a good knowledge on calculus (integration). Most of the students seem to have confusion regarding the use of the charge density. All you have to do is to just modify the latter part of the expression to bring the charge density into it to facilitate the integration to take place.