Question

Let R be the set of real numbers and $f:R\to R$ be given by $f\left( x \right)=\sqrt{\left| x \right|}-\log \left( 1+\left| x \right| \right)$. We now make the following assertions: I. There exists a real number $A$ such that $f\left( x \right)\le A$ for all $x$.
II. There exists a real number B such that $f\left( x \right)\ge B$ for all $x$.$A.I is true and II is false$
B.I is false and II is true$C.I and II both are true$
D.I and II both are false$$$$

Answer 1

We recall the definitions and critical points of a function and remember that maxima and minima of a function occur at the critical points. We use domain and range of the square root function and logarithmic function to conclude $\sqrt{\left| x \right|} > \log \left( 1+\left| x \right| \right)$ functions to conclude We try to find the critical points of the function to find $A$ and $B$. $$$$

Complete step-by-step solution:
We also know that the critical points of a function are the points where the first order derivative of the function is zero or the first derivative does not exist. Mathematically, $x=c$ is a critical point if $f'(c)=0$ or $f'(c)$ does not exist. The minima or maxima occur only at critical points. We are given the following real valued $f:R\to R$ function in the question $$f\left( x \right)=\sqrt{\left| x \right|}-\log \left( 1+\left| x \right| \right)$$ We see that we have a function which has two composite functions $\sqrt{\left| x \right|}$ and $\log \left( 1+\left| x \right| \right)$. We know that the first derivative of modulus function $\left| x \right|$ does not exist at $x=0$ and hence the first derivative of $f\left( x \right)$ will not exist at $x=0$. It makes $x=0$ a critical point of $f\left( x \right)$ and minima or maxima occur at $x=0$. We have $$f\left( 0 \right)=\sqrt{\left| 0 \right|}-\log \left( 1+\left| 0 \right| \right)=0$$ We know from the graph of the logarithmic function that $\log x\ge 0$ for all $x\ge 1$ and $\log x < 0$ for all $x\le 1$. Then we have $\log \left| x \right|\ge 0$ for all $\left| x \right|\ge 1$ and $\log x < 0$ for all $x < 1$. We further have $\log \left( 1+\left| x \right| \right)\ge 0$ for all $\left| x \right|\ge 0$. We know that square function is defined from ${{R}^{+}}$ to ${{R}^{+}}$. Hence $\sqrt{\left| x \right|}\ge 0$ for all $x\ge 0$. The zero of $f\left( x \right)$that is $x=0$ is the point of intersection $\sqrt{\left| x \right|},\log \left( 1+\left| x \right| \right)$.
We see that as we move away from left and right side of $x=0$and we shall get $f\left( x \right) > 0$ since $\sqrt{\left| x \right|} > \log \left( 1+\left| x \right| \right)$ for all $x > 0$. So $f\left( x \right)$ will have a minimum at $x=0$. There exists a real number $B=0$ such that $f\left( x \right)\ge B$ for all$x$. The plot of the function is below which is symmetrical about positive $y-$axis.  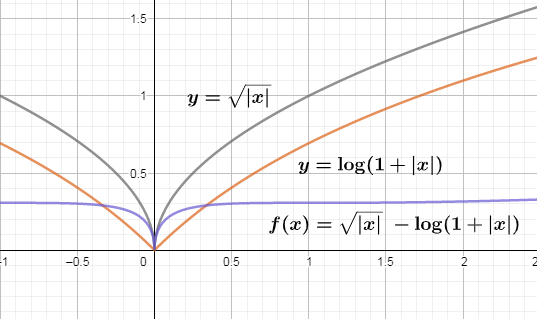We see that $f\left( x \right)$ does not have a maxima for all $x\in R$.So there does not exist an $A$ such that $f\left( x \right)\le A$. So the statement (I) is false and statement ((II) is true and hence option B is correct.

Note: We note that there is only one critical point of the function. We can also use the first derivative test here but that will be difficult. We also note that if $f\left( x \right)$ is a real valued single function defined within some interval $I\subset D$ , it will have its local maximum value (called maxima) $x=a$ when $f\left( a \right) < f\left( x \right)$ for all $x\in I$ and local minimum value $x=a$ (called minima) when $f\left( a \right) > f\left( x \right)$ for all $x\in I$.